想象一下,你站在拉斯维加斯的赌场里,面对着21点的牌桌。庄家正等着你做决定——要牌还是停牌。此刻的你,心中可能在快速计算着各种可能性。而在人工智能的世界里,有一种被称为蒙特卡洛方法的算法,正是通过类似的"试错学习"来掌握这种决策的艺术。
视频版:https://www.youtube.com/watch?v=W-CKlP6HzGA
今天,我想和你聊聊这个听起来很高大上,实际上却相当朴素的学习方法。它不需要什么高深的数学理论,也不需要对环境了如指掌,就能从一次次的实践中逐渐摸索出最优的策略。
从赌场到算法:蒙特卡洛的诞生传奇

蒙特卡洛方法的名字来源于摩纳哥的蒙特卡洛赌场,这个选择其实颇有深意。就像赌徒通过一次次下注来了解游戏规律一样,蒙特卡洛算法通过一次次完整的"游戏"来学习什么是好的决策。
在强化学习的框架下,蒙特卡洛方法属于无模型学习的范畴。什么叫无模型呢?简单说就是我们不需要事先知道环境的所有规则和概率分布。就像一个新手玩家坐到21点桌前,不需要背下所有的牌桌概率表,只需要一局一局地玩下去,观察每次决策的结果,逐渐形成自己的游戏策略。
根据强化学习领域的权威研究,这种方法的核心思想是通过采样完整的经验序列(我们称之为"episode")来估计状态或动作的价值函数。
无模型学习:从实践中来,到实践中去
传统的动态规划方法就像是一个全知的神,需要对环境的每一个细节都了若指掌。而蒙特卡洛方法更像是一个初来乍到的学徒,通过亲身体验来积累智慧。
这种差异体现在实际应用中就是,蒙特卡洛方法不需要环境模型,可以直接从与环境的交互中学习。这在很多现实场景中具有巨大优势,因为我们往往很难精确地建模复杂的真实环境。
想象你要学会投资股票。动态规划的思路是先搞清楚所有公司的财务状况、市场规律、经济周期等等,然后再开始投资。而蒙特卡洛的思路是,拿出一部分钱开始实际操作,记录每次投资决策的结果,通过不断试错来提升投资技巧。
MC预测:评估现有策略的价值
蒙特卡洛预测解决的问题是:给定一个策略,如何评估它的好坏?
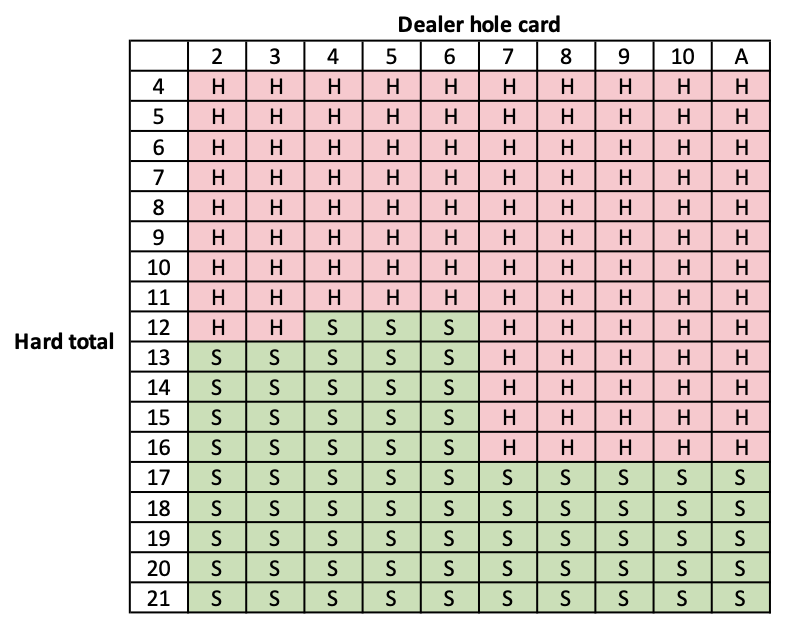
假设你已经有了一个21点的游戏策略:当手牌总和小于18时要牌,大于等于18时停牌。现在你想知道,在某个特定情况下(比如你手牌是14,庄家明牌是6),这个策略能带来多少收益。
首次访问蒙特卡洛方法会让你按照这个策略玩很多局游戏,每当第一次遇到"手牌14,庄家明牌6"这种情况时,就记录下从这个状态开始到游戏结束的总收益。玩得局数足够多后,这些收益的平均值就是该状态在当前策略下的价值估计。
而每次访问蒙特卡洛则更加"勤奋",不仅记录第一次遇到该状态的收益,而是记录每一次遇到时的收益。研究表明,两种方法都能收敛到真实的价值函数,但在实际应用中表现略有差异。
MC控制:寻找最优策略的智慧
如果说预测是评估现有策略,那么控制就是寻找更好的策略。这是蒙特卡洛方法真正展现威力的地方。
蒙特卡洛控制算法采用了一个经典的"策略迭代"思路:
- 从一个随机策略开始
- 用当前策略生成很多游戏经历
- 根据这些经历更新对各种状态-动作组合价值的估计
- 基于新的价值估计改进策略
- 重复上述过程直到收敛
这个过程就像是一个赌徒在不断优化自己的游戏策略。最初可能完全靠运气,但通过观察哪些决策带来了好结果,哪些带来了坏结果,逐渐调整自己的行为模式。
探索与利用:ε-greedy的平衡智慧
在学习过程中,有一个永恒的哲学问题:是应该坚持目前看起来最好的选择(利用),还是尝试一些新的可能性(探索)?
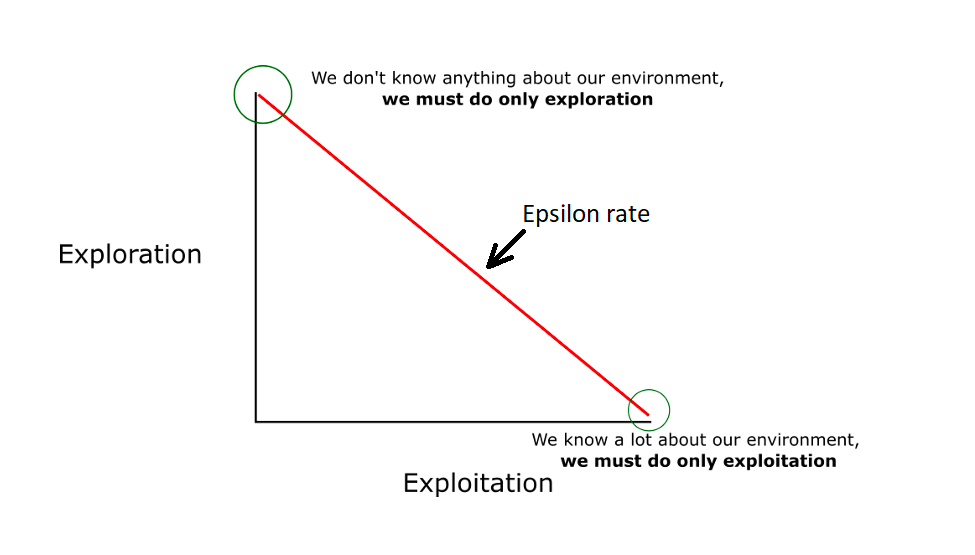
ε-贪心策略为这个问题提供了一个优雅的解决方案。它的思路很简单:大部分时候选择当前看起来最好的行动,但偶尔(以ε的概率)随机尝试其他行动。
在21点游戏中,这意味着算法大部分时候会选择当前策略认为最好的行动(比如在手牌总和为16时停牌),但偶尔也会"冒险"尝试其他选择(比如继续要牌),看看会发生什么。这种偶尔的"冒险"确保了算法不会过早地固化在一个局部最优的策略上。
研究数据显示,ε的取值对学习效果有显著影响。通常从较大的值(如0.1)开始,随着学习过程逐渐减小,让算法从"大胆探索"过渡到"精确利用"。
21点实战:从新手到高手的蜕变
让我们看看蒙特卡洛方法是如何征服21点游戏的。
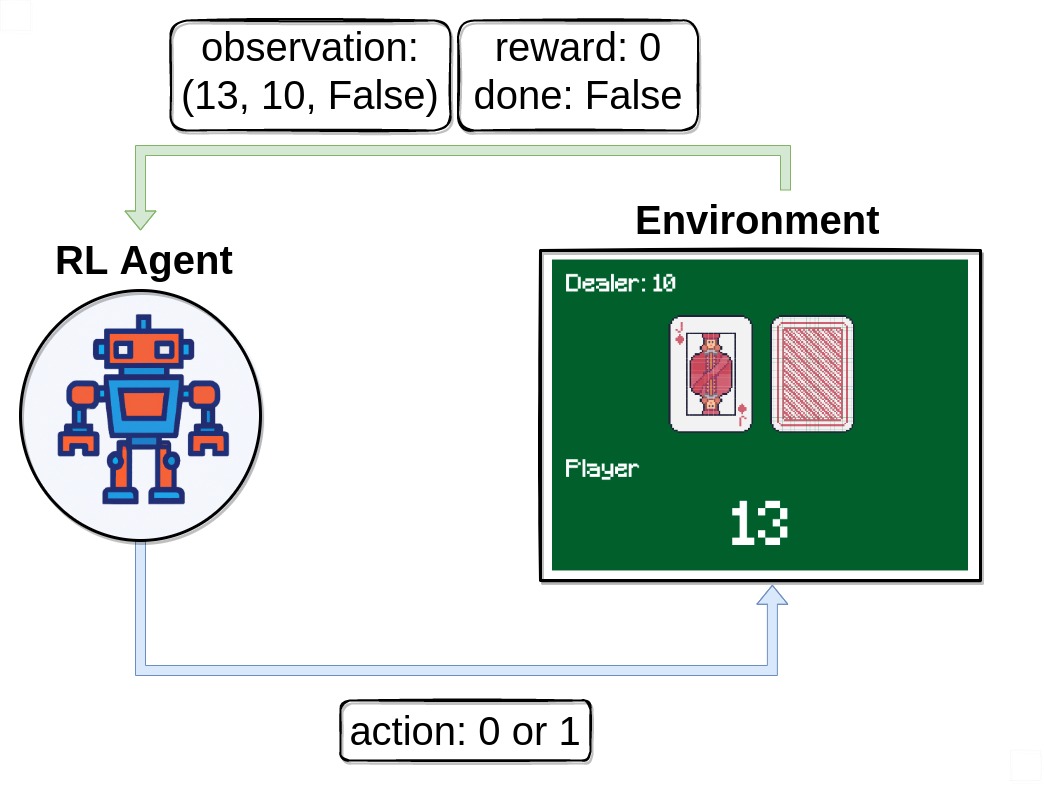
21点是一个相对简单但富有策略性的游戏,每个状态可以用三个信息描述:玩家手牌总和、庄家明牌、是否有可用的A牌。动作空间也很简单:要牌或停牌。
实际的学习过程是这样的:算法开始时几乎是随机行动,胜率大约在45%左右。但随着游戏局数的增加,它开始识别出一些模式。比如,当手牌总和为20时,继续要牌几乎总是导致失败;当手牌总和为11时,要牌往往是好选择。
经过大约50000局游戏的训练,蒙特卡洛算法的表现通常能达到专业玩家的水平,胜率稳定在49%左右(考虑到庄家的天然优势,这已经是相当不错的成绩)。
更有趣的是,我们可以观察到算法学习策略的演化过程。最初,它可能在所有情况下都倾向于要牌(因为这样"感觉"更积极)。但逐渐地,它学会了在手牌较大时保守停牌,在手牌较小时积极要牌,最终形成了与专业基本策略表高度一致的决策模式。
与动态规划的深度对比
要真正理解蒙特卡洛方法的价值,我们需要将它与动态规划进行对比。这两种方法就像是两种不同的学习哲学。
动态规划就像是一个理论派的学者,需要先搞清楚环境的所有规律,然后用数学公式推导出最优解。它的优点是一旦有了完整信息,收敛速度很快,而且是低方差的(结果比较稳定)。但问题是,现实世界中很难获得完整的环境模型。
蒙特卡洛方法则像是一个实践派的craftsman,通过反复试验来积累经验。它不需要环境模型,可以处理更复杂的情况,但代价是高方差和慢收敛。
在计算复杂度方面,如果环境有S个状态,动态规划的时间复杂度是O(S²)(需要考虑所有状态转移),而蒙特卡洛的复杂度主要取决于需要多少个episode来获得准确估计,这在高维状态空间中往往更有优势。
高方差问题:MC方法的阿喀琉斯之踵
蒙特卡洛方法最显著的缺点是高方差问题。为什么会出现这个问题呢?
想象你在评估一个投资策略的价值。动态规划方法会考虑所有可能的市场情况及其概率,给出一个"期望收益"。而蒙特卡洛方法只能基于历史上实际发生的情况。如果你碰巧遇到了几次市场大涨,可能会高估策略价值;如果遇到几次大跌,又可能低估。
研究数据表明,在同样的计算资源下,蒙特卡洛方法的价值估计标准差往往比动态规划高2-3倍。这意味着需要更多的样本才能获得稳定的估计。
但这个缺点在某些情况下也变成了优点。高方差意味着估计结果的不确定性更大,但同时也意味着对环境变化的敏感性更强。在非稳态环境中,这种敏感性反而有助于快速适应新情况。
完整Episode依赖:耐心的代价
蒙特卡洛方法的另一个特点是必须等到episode结束才能进行学习更新。这就像是你必须完整地看完一部电影才能评价它的好坏,不能中途下结论。
这种特性在某些应用场景中是优势。比如在游戏AI中,每局游戏都有明确的开始和结束,最终的胜负结果是唯一重要的评价标准。但在其他场景中,这种依赖可能成为限制。
想象一个自动驾驶系统,如果必须等到"一次完整的驾驶任务"结束才能学习,那学习效率会很低。这时候其他方法(如时间差分学习)可能更合适,因为它们可以在每一步都进行学习更新。
现代应用:从游戏到现实
虽然我们用21点作为例子,但蒙特卡洛方法的应用远不止于此。在现代AI领域,它在以下方面都有重要应用:
金融交易:蒙特卡洛方法被广泛用于期权定价和风险管理。交易员通过模拟成千上万种可能的市场情况来评估投资策略的风险和回报。
游戏AI:从国际象棋到围棋,蒙特卡洛树搜索(MCTS)已成为现代游戏AI的核心技术。AlphaGo的成功很大程度上归功于蒙特卡洛方法的应用。
资源调度:在云计算和网络管理中,蒙特卡洛方法帮助系统学习如何在不确定的负载模式下优化资源分配。
机器人学习:机器人通过不断尝试和犯错来学习复杂的操作技能,这正是蒙特卡洛方法的核心思想。
实现细节:从理论到代码
当我们要实现一个蒙特卡洛控制算法时,有几个关键的技术细节需要注意:
学习率的选择:传统的蒙特卡洛使用样本平均,但在实践中,使用固定学习率α往往效果更好。α=0.01到0.1是常见的选择范围。
ε衰减策略:ε不应该保持恒定,而应该随着学习过程逐渐减小。常见的衰减策略包括线性衰减(ε = ε₀ × (1 – t/T))和指数衰减(ε = ε₀ × γᵗ)。
状态表示:在21点中,状态可以简单地用元组表示,但在更复杂的环境中,可能需要函数近似(如神经网络)来处理高维状态空间。
代码实现通常包含以下核心组件:策略类、价值函数表、episode生成器、和策略更新器。整个算法的核心循环就是不断生成episode、计算回报、更新价值函数、改进策略。
未来展望:MC方法的演进之路
虽然基础的蒙特卡洛方法已经诞生了几十年,但它仍在不断演进:
深度蒙特卡洛:结合深度学习的蒙特卡洛方法可以处理更复杂的状态空间,这在图像识别和自然语言处理中有重要应用。
分布式蒙特卡洛:通过并行计算技术,可以同时运行多个蒙特卡洛模拟,大大提高学习效率。
自适应采样:现代变种能够智能地调整采样策略,在重要的状态-动作对上投入更多计算资源。
混合方法:将蒙特卡洛与其他方法(如时间差分学习)结合,扬长避短,在保持无模型优势的同时降低方差。
哲学思考:学习的本质
从更深层次来看,蒙特卡洛方法体现了一种朴素而深刻的学习哲学:通过经验来获得智慧。
这种思想与人类的学习过程高度一致。我们不是通过背诵理论来学会骑自行车的,而是通过一次次摔倒和爬起来。我们不是通过研究心理学教科书来学会社交的,而是通过与人交往中的成功和失败。
蒙特卡洛方法告诉我们,即使在信息不完整、环境不确定的情况下,只要有足够的耐心和合适的方法,我们仍然可以逐步接近最优解。这不仅是一个算法原理,更是一种生活态度。
在这个充满不确定性的世界里,我们每个人都像是在执行着自己的蒙特卡洛算法。我们在工作中尝试不同的方法,在人际关系中探索不同的沟通方式,在投资中测试不同的策略。每一次经历都是一个"episode",每一次反思都是一次"价值更新"。
而ε-贪心策略提醒我们,即使在已经找到了看似不错的解决方案时,也要保持一定的开放性和好奇心,偶尔尝试一些新的可能性。因为真正的最优解可能就隐藏在那些我们尚未探索的角落。
写在最后
蒙特卡洛方法美妙地平衡了简单性和有效性。它不需要复杂的数学推导,不需要完美的环境模型,却能够解决许多现实世界的复杂问题。
当你下次面对一个充满不确定性的决策时,不妨想想蒙特卡洛的智慧:不要试图一开始就找到完美答案,而是勇敢地开始行动,从每次经历中学习,逐步改进你的策略。就像那些在拉斯维加斯学会21点的AI一样,真正的智慧往往来自于实践中的点滴积累。
正如那句古话所说:"熟能生巧"。而蒙特卡洛方法,正是将这个朴素的道理精确地量化成了算法。在这个意义上,它不仅是一种计算方法,更是一种学习和成长的哲学。