想象一下,你是一位医生,面对一个病人的检查结果。传统的诊断方法可能会告诉你:"这个病人有80%的概率患有某种疾病。"但如果你是一位贝叶斯主义者,你会说:"基于我之前的经验和这次的检查结果,我对这个诊断的确信程度是这样的…"这种微妙的差别,正是贝叶斯机器学习的魅力所在。
页面版:https://www.genspark.ai/api/page_private?id=ewzipuju
视频版:https://www.youtube.com/watch?v=2rMPrVPzt58
音频版:https://notebooklm.google.com/notebook/6f696f82-3c3d-42c2-80f5-a3afbcc82878/audio
当不确定性成为朋友
在机器学习的世界里,大多数时候我们都在与不确定性作斗争。传统的频率派方法就像一个固执的老师,总是给出一个确定的答案。而贝叶斯方法则像一个智慧的哲学家,它不仅给出答案,还告诉你这个答案有多可靠。
DataRobot的研究指出,贝叶斯机器学习的核心在于估计后验分布p(θ|x),而不是简单地找到一个最优的参数值。这种方法让我们能够量化预测的不确定性,在医疗诊断、金融风控等高风险领域尤其有价值。

三个关键角色的故事
贝叶斯定理就像一个精彩的三角关系故事,主角是先验(Prior)、似然(Likelihood)和后验(Posterior)。
先验就像你的第一印象。假设你要预测明天会不会下雨,你的先验知识可能来自于"这个季节通常很少下雨"这样的历史经验。数学上,我们用p(θ)来表示这种先验信念。
似然则是新证据的声音。当你看到今天乌云密布、湿度很高时,这些观察到的数据会更新你的判断。似然函数p(x|θ)描述了在给定参数θ的情况下,观察到数据x的概率。
后验是智慧的结晶。它综合了你的先验知识和新观察到的证据,给出了一个更加准确的判断。根据贝叶斯定理:
p(θ|x) = p(x|θ)p(θ) / p(x)
这个看似简单的公式,却蕴含着深刻的哲学思想:我们的认知应该随着新证据的出现而不断更新。
MCMC:概率世界的探险家
当我们想要从复杂的后验分布中采样时,直接计算往往是不可能的。这时候,马尔可夫链蒙特卡洛(MCMC)方法就像一个勇敢的探险家,帮助我们在高维参数空间中寻找宝藏。
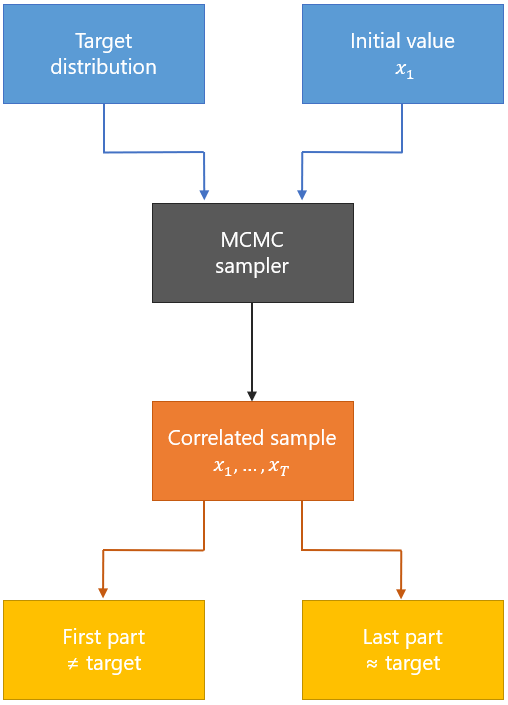
MCMC方法的巧妙之处在于,它构造了一个马尔可夫链,这个链的平稳分布正好是我们想要的后验分布。最经典的Metropolis-Hastings算法就像一个谨慎的登山者,每次都会评估新的位置是否比当前位置更好,如果更好就移动过去,如果不好就以一定的概率决定是否移动。
这种看似随机的"游走"过程,实际上是一种非常聪明的策略。经过足够长的时间,我们就能够获得后验分布的准确样本。
变分推断:优化的艺术
如果说MCMC是探险家,那么变分推断(Variational Inference)就是一位精明的商人。它不会花费大量时间去寻找精确的答案,而是通过优化技巧找到一个"足够好"的近似解。
变分推断的核心思想是将推断问题转化为优化问题。我们定义一个简单的分布族(比如高斯分布),然后通过最小化KL散度来找到最接近真实后验分布的近似分布。
这种方法的优势在于速度快、可扩展性强,特别适合大数据场景。虽然它可能不如MCMC那样精确,但在很多实际应用中,这种权衡是非常值得的。
高斯过程:函数空间的贝叶斯
当我们谈论回归问题时,传统方法是选择一条最佳拟合线。但是高斯过程(Gaussian Process)有一个更加浪漫的想法:为什么不考虑所有可能的函数,然后选择最合理的那一个?
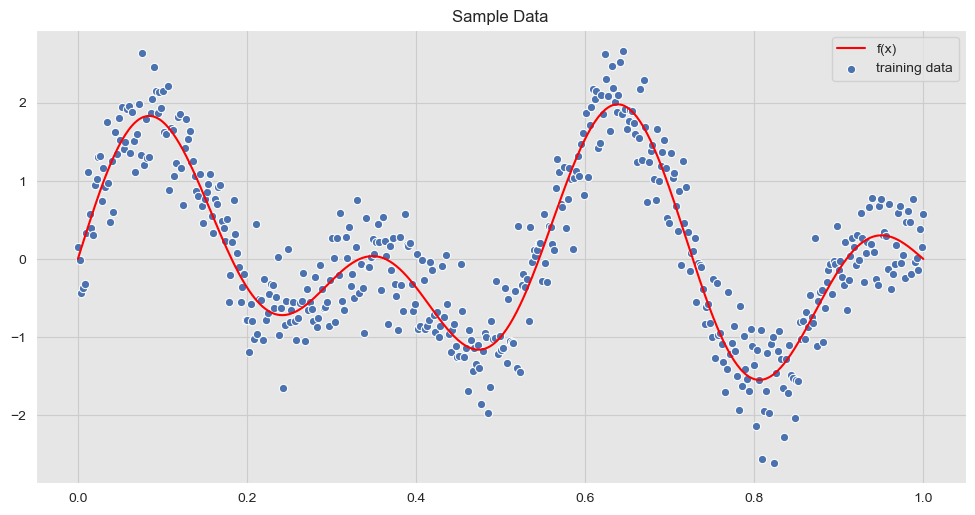
高斯过程就像一个函数的概率分布。它不仅给出预测值,还给出了预测的不确定性。当你有很多训练数据时,预测的不确定性会很小;当你进入未知领域时,不确定性会增大。这种特性使得高斯过程在主动学习、优化等领域有着广泛的应用。
Rasmussen和Williams的经典著作详细介绍了高斯过程的理论基础。高斯过程的核函数决定了函数的性质,比如光滑性、周期性等。通过选择合适的核函数,我们可以编码我们对函数形状的先验知识。
频率派与贝叶斯派的哲学对话
在机器学习的世界里,频率派和贝叶斯派就像两个不同的哲学学派。频率派认为参数是固定的,数据是随机的;贝叶斯派则认为参数是不确定的,数据是观察到的事实。
这种差异在实际应用中有着深远的影响。当你只有很少的训练数据时,频率派方法可能会过拟合,而贝叶斯方法通过先验知识的正则化效应,往往能够给出更加稳健的结果。
近期的研究表明,在参数估计和模型选择任务中,变分推断可以作为MCMC的有效替代方案,特别是在大规模数据集上。这种方法的计算效率显著提高,同时保持了合理的准确性。
实践中的智慧
让我们来看一个具体的例子。假设你要预测房价,你有一些历史数据,但数据量不大。传统的线性回归可能会给你一个确定的预测:"这套房子价值50万元。"
但是贝叶斯线性回归会告诉你:"基于现有数据,我认为这套房子的价值在45万到55万之间,其中50万的概率最大。"这种表达方式显然更加诚实和有用。
使用PyMC3或Pyro这样的概率编程库,我们可以很容易地实现贝叶斯模型。这些库提供了高级的抽象,让我们能够专注于模型设计而不是底层的采样算法。
医学诊断中的贝叶斯智慧
在医学诊断领域,贝叶斯方法展现出了独特的价值。当面对一个罕见疾病的检测时,即使检测的准确率很高,如果疾病的患病率很低,那么阳性结果的可信度可能并不高。
这就是著名的"基率忽略"问题。贝叶斯定理帮助我们正确地整合先验概率(疾病的患病率)和新证据(检测结果),从而做出更加准确的诊断。
金融风控的概率视角
在金融领域,不确定性是常态。传统的信用评分模型可能会说:"这个客户的违约概率是5%。"但贝叶斯模型会说:"基于当前信息,我对这个客户违约概率的估计是5%,但这个估计本身的不确定性区间是3%到7%。"
这种细致的不确定性量化,对于风险管理来说是非常宝贵的。它不仅告诉我们风险的大小,还告诉我们对这个风险估计的信心程度。
未来的展望
随着计算能力的提升和算法的改进,贝叶斯机器学习正在迎来新的春天。自动微分变分推断(ADVI)、正规化流(Normalizing Flows)等新技术,使得贝叶斯方法在深度学习等复杂模型中的应用成为可能。
深度学习中的贝叶斯神经网络,不仅能够给出预测结果,还能够量化预测的不确定性。这在自动驾驶、医疗诊断等安全攸关的应用中尤其重要。
贝叶斯机器学习教给我们的不仅仅是一套技术方法,更是一种思维方式:在面对不确定性时,我们应该诚实地承认自己的无知,同时理性地利用已有的信息。正如一位哲学家所说:"智者知道自己无知。"在机器学习的世界里,贝叶斯方法正是这种智慧的体现。
在这个数据爆炸的时代,我们需要的不是更多的确定性,而是更好地理解和处理不确定性。贝叶斯机器学习为我们提供了这样一个框架,让我们能够在不确定的世界中做出更加明智的决策。