如果你曾经好奇过人工智能是如何"思考"的,那么神经网络的故事就像一个科学版的创世纪。想象一下,在1943年,当世界还在二战硝烟中时,两位科学家Warren McCulloch和Walter Pitts却在思考一个看似天马行空的问题:能否用数学公式来模拟人类大脑的工作原理?
这个问题的答案,后来改变了整个世界。
网页版:https://qvgfzmry.gensparkspace.com/
视频版:https://www.youtube.com/watch?v=AwzkCZEPbjM
音频版:https://notebooklm.google.com/notebook/2c251c05-33e9-432b-b299-920750ec47e7/audio
生物神经元的启发:从大脑到硅片的奇迹
让我们先来看看大脑中的真正"主角"——生物神经元。每个神经元就像一个微型的信息处理工厂,它有着令人惊叹的结构:细胞体负责处理信息,树突像触角一样接收来自其他神经元的信号,而轴突则像高速公路,将处理后的信号传递给下一个神经元。

人类大脑包含约1000亿个神经元,每个神经元平均与7000个其他神经元连接。这意味着我们的大脑中有大约700万亿个连接,这个数字比银河系中的恒星数量还要多。
但是,正如Meta的首席AI科学家Yann LeCun所说:"虽然飞机的灵感来自鸟类,但它们不需要拍打翅膀。"人工神经网络同样如此,它们受到生物神经元的启发,但采用了完全不同的实现方式。
感知机的诞生:人工神经元的第一次尝试
1957年,Frank Rosenblatt在康奈尔大学提出了感知机(Perceptron)的概念。这是一个看起来简单得几乎可爱的数学模型:它接收多个输入信号,给每个信号分配一个权重,然后计算加权和。如果这个和超过某个阈值,感知机就"激活";否则就保持沉默。

用数学公式表示就是:
输出 = 1 如果 Σ(权重i × 输入i) > 阈值
输出 = 0 如果 Σ(权重i × 输入i) ≤ 阈值
这个简单的模型却有着惊人的能力。感知机可以实现AND、OR、NAND等基本逻辑运算,而由于NAND门具有计算完备性,理论上感知机网络可以实现任何计算功能。
但是,感知机也有一个致命的缺陷:它只能处理线性可分的数据。想象一下,如果你需要在二维平面上用一条直线来分离两类点,感知机就能完成这个任务。但如果这两类点交错分布,无法用直线分离,感知机就束手无策了。
多层感知机:突破线性限制的革命
感知机的局限性在1969年被Marvin Minsky和Seymour Papert在他们的著作《Perceptrons》中详细阐述,这几乎让神经网络研究陷入了长达十几年的"AI寒冬"。
但是,科学家们并没有放弃。他们发现,如果将多个感知机层叠起来,就能创造出处理非线性问题的能力。这就是多层感知机(Multi-Layer Perceptron, MLP)的诞生。

多层感知机的核心思想是:第一层神经元做出简单的决策,第二层神经元基于第一层的结果做出更复杂的决策,以此类推。这种层次化的决策过程,让网络能够学习复杂的非线性模式。
激活函数:神经网络的灵魂
但是,仅仅堆叠线性层并不能解决非线性问题。关键在于激活函数的引入。激活函数就像是神经网络的"个性",它决定了神经元如何响应输入。
最常用的激活函数是Sigmoid函数:
σ(x) = 1 / (1 + e^(-x))

Sigmoid函数的美妙之处在于它的平滑性。与感知机的硬阈值不同,Sigmoid函数提供了一个平滑的过渡,这意味着输入的小变化只会导致输出的小变化。这个特性对于网络的学习过程至关重要。
反向传播:让机器学会学习的魔法
有了多层结构和激活函数,下一个问题就是:如何训练这个复杂的网络?答案就是反向传播算法(Backpropagation),这个算法在1986年由David Rumelhart、Geoffrey Hinton和Ronald Williams重新发现并系统化。
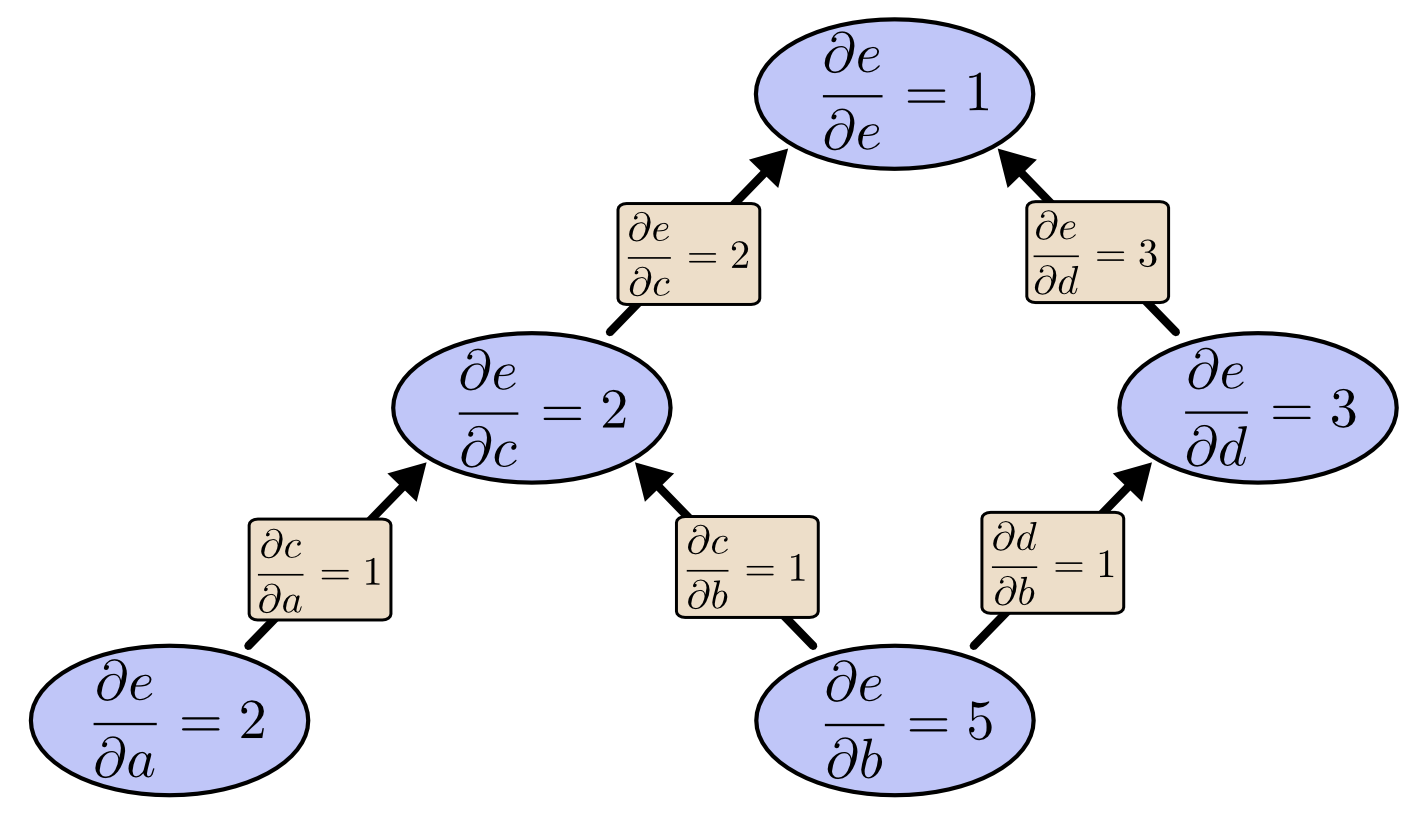
反向传播算法的核心思想是利用链式法则来计算梯度。想象一下,网络的每个权重都像是一个旋钮,我们需要知道调整每个旋钮会如何影响最终的输出错误。
算法的工作流程是这样的:
- 前向传播:输入数据通过网络,计算出预测结果
- 计算损失:比较预测结果和真实标签,计算错误
- 反向传播:从输出层开始,逐层计算每个权重对总错误的贡献
- 更新权重:根据梯度信息调整权重,减少错误
这个过程就像是在黑暗中摸索下山的路径,每次都朝着错误减少最快的方向前进。
手写数字识别:从理论到实践的华丽转身
理论说得再好,也需要实践来验证。MNIST手写数字识别数据集就是神经网络的"Hello World"项目。

MNIST数据集包含70,000个手写数字图像,每个图像都是28×28像素的灰度图。这些图像来自美国人口普查局员工和高中生的手写样本。
实现一个简单的多层感知机来识别手写数字的过程非常有趣:
class SimpleMLP:
def __init__(self, input_size=784, hidden_size=128, output_size=10):
# 初始化权重
self.W1 = np.random.randn(input_size, hidden_size) * 0.01
self.b1 = np.zeros((1, hidden_size))
self.W2 = np.random.randn(hidden_size, output_size) * 0.01
self.b2 = np.zeros((1, output_size))
def forward(self, X):
# 前向传播
self.z1 = np.dot(X, self.W1) + self.b1
self.a1 = self.sigmoid(self.z1)
self.z2 = np.dot(self.a1, self.W2) + self.b2
self.a2 = self.softmax(self.z2)
return self.a2
当我们训练这个网络时,会发现一个令人惊叹的现象:即使是一个简单的两层网络,也能达到96%以上的准确率。这意味着在10,000个测试图像中,只有不到400个被错误分类。
决策边界:从线性到非线性的视觉革命
为了更好地理解多层网络的强大之处,我们可以可视化它们的决策边界。

单层感知机只能创建线性决策边界,这就像用一把直尺在纸上画线来分离不同的区域。但是多层网络可以创建复杂的非线性决策边界,就像一个灵活的画家,能够绘制出任意形状的分离线。
这种能力的关键在于隐藏层的作用。每个隐藏层神经元都在寻找输入数据的特定模式,然后输出层将这些模式组合起来做出最终决策。
梯度流动:理解网络学习的内在机制
反向传播算法的美妙之处在于梯度在网络中的流动方式。

梯度就像是水流,从输出层开始,沿着网络的连接向后流动。每个权重都会根据它对最终错误的贡献程度来调整自己的值。这个过程遵循链式法则:
∂Loss/∂W1 = ∂Loss/∂a2 × ∂a2/∂z2 × ∂z2/∂a1 × ∂a1/∂z1 × ∂z1/∂W1
这个公式看起来复杂,但实际上它只是在告诉我们:要知道调整第一层权重对损失的影响,我们需要追踪这个影响如何通过网络的每一层传播。
从手工推导到自动求导:现代工具的力量
虽然手工推导BP算法对理解很有帮助,但在实际应用中,我们通常使用PyTorch或TensorFlow等框架的自动求导功能。
import torch
import torch.nn as nn
class MLP(nn.Module):
def __init__(self, input_size=784, hidden_size=128, output_size=10):
super(MLP, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.fc2 = nn.Linear(hidden_size, output_size)
self.relu = nn.ReLU()
def forward(self, x):
x = self.relu(self.fc1(x))
x = self.fc2(x)
return x
model = MLP()
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
PyTorch的自动求导引擎可以自动计算任何可微分函数的梯度,这让我们可以专注于网络架构设计,而不必担心复杂的数学推导。
现代深度学习的基石
从最初的感知机到现在的深度学习,这个进化过程展现了科学研究的迷人之处。今天最先进的神经网络,如GPT、BERT等,都是建立在这些基础概念之上的。
现代银行使用神经网络来处理支票,邮局用它们来识别地址,这些都是从最初的MNIST数字识别发展而来的。每一次技术的飞跃,都是站在前人的肩膀上。
未来的展望
从感知机到多层网络的这段旅程,不仅仅是一个技术发展的故事,更是人类智慧不断突破自身限制的见证。当我们理解了这些基本原理之后,就能更好地欣赏现代AI技术的精妙之处。
下一次当你看到AI在下棋、写诗、画画时,记住这一切都源于那个简单而美妙的想法:用数学来模拟大脑的工作原理。而这个想法,正在一步步改变着我们的世界。