在某个寒冷的冬日,我迷上了一个简单得不能再简单的游戏:让一个小方块在网格世界中寻找到出口。这个游戏本身没什么特别的,但当我开始思考如何让计算机自己学会玩这个游戏时,一扇通往强化学习世界的大门悄然打开。
网页版:https://www.genspark.ai/api/page_private?id=tegpyvcy
视频版:https://www.youtube.com/watch?v=aLmSIjnRvfg
音频版:https://notebooklm.google.com/notebook/d23267f2-282b-4a4a-b418-6564dff8f35c/audio
或许你已经听说过机器学习,但强化学习(Reinforcement Learning,RL)作为其中一个分支,有着独特的魅力。它不像监督学习那样需要大量标记数据,也不像无监督学习那样只关注数据的内在结构。强化学习更像是一种通过"试错"来学习的方法,就像我们人类学习骑自行车一样——摔倒几次,慢慢就掌握了平衡的诀窍。
今天,我想和你分享这段奇妙的探索之旅,从基本概念到算法实现,再到实际应用,看看强化学习如何从解决简单的迷宫问题,进化到挑战Atari经典游戏。
当智能体遇上环境:强化学习的基本概念
想象一下,你有一个机器人(我们称之为"智能体",Agent)放在一个迷宫中(称为"环境",Environment)。这个机器人的目标是找到出口,但它对迷宫一无所知。它唯一能做的就是:观察当前位置(状态,State)、决定往哪个方向移动(动作,Action),然后获得某种反馈(奖励,Reward)。
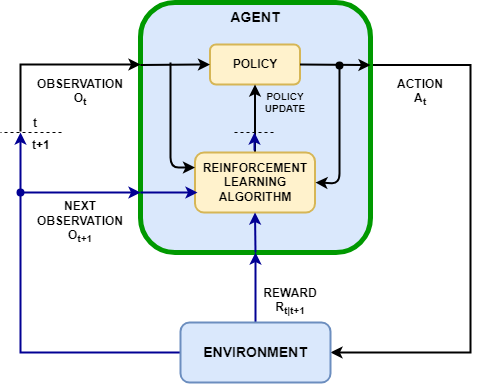
这就是强化学习的核心场景。在这个过程中:
- 智能体(Agent):做决策的实体,比如我们的迷宫机器人
- 环境(Environment):智能体所处的世界,如迷宫
- 状态(State):环境的当前情况,如机器人在迷宫中的位置
- 动作(Action):智能体可以采取的行为,如向上、下、左、右移动
- 奖励(Reward):环境给予智能体的反馈,如接近出口+1分,撞墙-1分
- 策略(Policy):智能体的行为方式,决定在特定状态下采取什么动作
- 价值函数(Value Function):评估状态或动作的价值,预测未来可能获得的累积奖励
刚开始时,我们的机器人会随机移动,偶尔撞墙,偶尔走向死胡同。但随着时间推移,它会慢慢学会哪些动作会带来更多奖励,逐渐形成一个有效的策略。这种从尝试中学习的过程,正是强化学习的精髓。
我最初被强化学习吸引,就是因为它这种近乎"人性化"的学习方式。没有人告诉机器人具体怎么走,它完全靠自己的探索和经验总结,最终掌握了解决问题的能力。这不正是我们人类学习的方式吗?
马尔可夫决策过程:强化学习的数学框架
当我们深入研究强化学习时,很快会遇到一个重要的数学工具:马尔可夫决策过程(Markov Decision Process,MDP)。这个名字听起来很复杂,但概念其实很直观。
MDP是一个五元组(S, A, P, R, γ),其中:
- S:所有可能的状态集合
- A:所有可能的动作集合
- P:状态转移概率,即采取某个动作后环境状态改变的概率
- R:奖励函数,即在某个状态采取某个动作后获得的即时奖励
- γ:折扣因子,用于平衡即时奖励和未来奖励的重要性
马尔可夫性质是指:下一个状态只取决于当前状态和动作,而与历史路径无关。这个假设大大简化了问题,使得我们可以用数学方法求解最优策略。
在我的迷宫例子中,状态就是机器人的位置,动作是四个移动方向,状态转移是确定性的(向左移动就一定会到左边的格子,除非有墙),奖励是根据是否接近出口而定义的。
MDP的目标是找到一个策略π,使得从任何起始状态开始,按照这个策略行动能获得的期望累积奖励最大化。这个累积奖励通常表示为:

其中Rt是在时间步t获得的奖励,γ是折扣因子(0≤γ≤1)。
对于像国际象棋这样的游戏,状态空间可能非常庞大(10^50级别的状态),如果用表格来存储每个状态的价值,不仅内存不够,计算量也是天文数字。这就是为什么我们需要函数近似方法,比如深度学习网络来表示价值函数或策略。
贝尔曼方程:从现在到未来的桥梁
贝尔曼方程是强化学习中另一个核心概念,它建立了当前状态价值与未来状态价值之间的关系。这个方程看起来可能有点吓人,但本质上是一个递归定义:
一个状态的价值等于在这个状态下采取最优动作后,即时获得的奖励,加上下一个状态的折扣价值的期望。
数学表达式为:
V(s) = max_a [R(s,a) + γ∑_s’ P(s’|s,a)V(s’)]
对于状态-动作价值函数Q(s,a),贝尔曼方程为:
Q(s,a) = R(s,a) + γ∑_s’ P(s’|s,a)max_a’ Q(s’,a’)
当我第一次理解贝尔曼方程时,仿佛有一道光照进了迷雾。它优雅地解决了"如何评估长期利益"这个问题。比如在迷宫中,某些看似远离目标的移动可能最终是最优路径的一部分。贝尔曼方程让我们能够递归地评估每个决策的长期价值。
以下是贝尔曼方程在实际应用中的可视化示例:

Q-Learning:从理论到实践的跨越
理解了基本概念和数学框架后,是时候介绍一个实用的算法了:Q-Learning。这是一种无模型(model-free)的强化学习算法,意味着它不需要知道环境的转移概率和奖励函数,可以直接从与环境的交互中学习。
Q-Learning的核心思想是学习一个Q表(Q-table),表中存储了每个状态-动作对(s,a)的价值Q(s,a)。学习过程使用以下更新规则:
Q(s,a) ← Q(s,a) + α[r + γ·max_a’ Q(s’,a’) – Q(s,a)]
其中:
- α是学习率,控制更新的步长
- r是即时奖励
- γ是折扣因子
- max_a’ Q(s’,a’)是下一个状态s’中所有可能动作的最大Q值
Q-Learning算法的步骤如下:
- 初始化Q表,对所有状态-动作对(s,a),设置Q(s,a) = 0
- 对于每个回合(episode):
a. 观察当前状态s
b. 基于ε-贪婪策略选择动作a(以ε的概率随机探索,以1-ε的概率选择当前最优动作)
c. 执行动作a,观察奖励r和新状态s’
d. 更新Q表:Q(s,a) ← Q(s,a) + α[r + γ·max_a’ Q(s’,a’) – Q(s,a)]
e. s ← s’
f. 如果s是终止状态,结束当前回合
下面是一个使用PyTorch实现Q-Learning的简单示例代码,用于解决一个网格世界问题:
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
import random
from collections import deque
# 定义一个简单的网格世界环境
class GridWorld:
def __init__(self, size=5):
self.size = size
self.reset()
# 障碍物位置
self.obstacles = [(1, 1), (2, 2), (3, 1)]
# 目标位置
self.goal = (4, 4)
def reset(self):
self.agent_pos = (0, 0)
self.done = False
return self._get_state()
def _get_state(self):
# 状态编码:将二维位置编码为一维索引
return self.agent_pos[0] * self.size + self.agent_pos[1]
def step(self, action):
# 0: 上, 1: 右, 2: 下, 3: 左
directions = [(-1, 0), (0, 1), (1, 0), (0, -1)]
# 计算新位置
new_pos = (self.agent_pos[0] + directions[action][0],
self.agent_pos[1] + directions[action][1])
# 检查是否越界或撞到障碍物
if (0 <= new_pos[0] < self.size and
0 <= new_pos[1] < self.size and
new_pos not in self.obstacles):
self.agent_pos = new_pos
# 计算奖励
if self.agent_pos == self.goal:
reward = 1.0
self.done = True
else:
reward = -0.01 # 小的负奖励鼓励寻找最短路径
return self._get_state(), reward, self.done
# 定义Q网络
class QNetwork(nn.Module):
def __init__(self, state_size, action_size):
super(QNetwork, self).__init__()
self.fc1 = nn.Linear(state_size, 64)
self.fc2 = nn.Linear(64, 64)
self.fc3 = nn.Linear(64, action_size)
def forward(self, state):
x = torch.relu(self.fc1(state))
x = torch.relu(self.fc2(x))
return self.fc3(x)
# 定义经验回放缓冲区
class ReplayBuffer:
def __init__(self, capacity):
self.buffer = deque(maxlen=capacity)
def add(self, state, action, reward, next_state, done):
self.buffer.append((state, action, reward, next_state, done))
def sample(self, batch_size):
return random.sample(self.buffer, batch_size)
def __len__(self):
return len(self.buffer)
# 定义DQN智能体
class DQNAgent:
def __init__(self, state_size, action_size):
self.state_size = state_size
self.action_size = action_size
# Q网络
self.q_network = QNetwork(state_size, action_size)
self.target_network = QNetwork(state_size, action_size)
self.target_network.load_state_dict(self.q_network.state_dict())
# 优化器
self.optimizer = optim.Adam(self.q_network.parameters(), lr=0.001)
# 经验回放
self.replay_buffer = ReplayBuffer(10000)
# 超参数
self.batch_size = 64
self.gamma = 0.99 # 折扣因子
self.epsilon = 1.0 # 探索率
self.epsilon_decay = 0.995
self.epsilon_min = 0.01
self.update_target_every = 100
self.train_count = 0
def act(self, state):
# ε-贪婪策略
if np.random.rand() < self.epsilon:
return random.randrange(self.action_size)
state_tensor = torch.FloatTensor(np.eye(self.state_size)[state]).unsqueeze(0)
with torch.no_grad():
action_values = self.q_network(state_tensor)
return torch.argmax(action_values).item()
def train(self):
if len(self.replay_buffer) < self.batch_size:
return
# 从经验回放中采样
batch = self.replay_buffer.sample(self.batch_size)
# 提取批次数据
states = np.array([np.eye(self.state_size)[b[0]] for b in batch])
actions = np.array([b[1] for b in batch])
rewards = np.array([b[2] for b in batch])
next_states = np.array([np.eye(self.state_size)[b[3]] for b in batch])
dones = np.array([b[4] for b in batch])
# 转换为张量
state_tensor = torch.FloatTensor(states)
action_tensor = torch.LongTensor(actions).unsqueeze(1)
reward_tensor = torch.FloatTensor(rewards).unsqueeze(1)
next_state_tensor = torch.FloatTensor(next_states)
done_tensor = torch.FloatTensor(dones).unsqueeze(1)
# 计算当前Q值
current_q = self.q_network(state_tensor).gather(1, action_tensor)
# 计算目标Q值
with torch.no_grad():
next_q = self.target_network(next_state_tensor).max(1)[0].unsqueeze(1)
target_q = reward_tensor + (1 - done_tensor) * self.gamma * next_q
# 计算损失
loss = nn.MSELoss()(current_q, target_q)
# 优化
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
# 更新目标网络
self.train_count += 1
if self.train_count % self.update_target_every == 0:
self.target_network.load_state_dict(self.q_network.state_dict())
# 衰减探索率
if self.epsilon > self.epsilon_min:
self.epsilon *= self.epsilon_decay
# 训练智能体
def train_agent():
env = GridWorld(size=5)
state_size = env.size * env.size
action_size = 4
agent = DQNAgent(state_size, action_size)
num_episodes = 1000
max_steps = 100
rewards_history = []
for episode in range(num_episodes):
state = env.reset()
total_reward = 0
for step in range(max_steps):
action = agent.act(state)
next_state, reward, done = env.step(action)
agent.replay_buffer.add(state, action, reward, next_state, done)
agent.train()
state = next_state
total_reward += reward
if done:
break
rewards_history.append(total_reward)
if episode % 100 == 0:
print(f"Episode {episode}/{num_episodes}, Avg Reward: {np.mean(rewards_history[-100:]):.2f}, Epsilon: {agent.epsilon:.2f}")
return agent, rewards_history
# 可视化训练结果
def plot_rewards(rewards):
plt.figure(figsize=(10, 6))
plt.plot(rewards)
plt.title('训练奖励')
plt.xlabel('回合')
plt.ylabel('总奖励')
plt.grid(True)
plt.show()
# 可视化学习到的策略
def visualize_policy(agent, env):
policy = np.zeros((env.size, env.size), dtype=int)
for i in range(env.size):
for j in range(env.size):
state = i * env.size + j
state_tensor = torch.FloatTensor(np.eye(agent.state_size)[state]).unsqueeze(0)
with torch.no_grad():
action_values = agent.q_network(state_tensor)
policy[i, j] = torch.argmax(action_values).item()
# 创建策略可视化
fig, ax = plt.subplots(figsize=(8, 8))
# 绘制网格
for i in range(env.size + 1):
ax.axhline(i, color='black', lw=1)
ax.axvline(i, color='black', lw=1)
# 绘制障碍物
for obs in env.obstacles:
ax.add_patch(plt.Rectangle((obs[1], obs[0]), 1, 1, fill=True, color='gray'))
# 绘制目标
ax.add_patch(plt.Rectangle((env.goal[1], env.goal[0]), 1, 1, fill=True, color='green', alpha=0.5))
# 绘制策略箭头
arrows = ['↑', '→', '↓', '←']
for i in range(env.size):
for j in range(env.size):
if (i, j) in env.obstacles or (i, j) == env.goal:
continue
ax.text(j + 0.5, i + 0.5, arrows[policy[i, j]],
horizontalalignment='center', verticalalignment='center', fontsize=20)
ax.set_title('学习到的策略')
ax.set_xticks([])
ax.set_yticks([])
plt.tight_layout()
plt.show()
# 主函数
if __name__ == "__main__":
agent, rewards = train_agent()
plot_rewards(rewards)
env = GridWorld(size=5)
visualize_policy(agent, env)
这段代码虽然看起来复杂,但其核心就是Q-Learning算法的实现。通过这个例子,我们可以看到强化学习算法如何在实际中应用,以及如何使用神经网络替代传统的Q表来处理更复杂的问题。
深度Q网络(DQN):挑战Atari游戏
虽然Q-Learning在简单环境中表现出色,但当状态空间变得非常大时(比如在视频游戏中,每个像素都是状态的一部分),传统的Q表方法就显得力不从心了。这就是深度Q网络(Deep Q-Network,DQN)出场的时刻。
DQN将Q-Learning与深度神经网络相结合,使用神经网络来近似Q函数,而不是用表格存储每个状态-动作对的Q值。2013年,DeepMind团队使用DQN训练了一个能玩Atari游戏的AI,引起了学术界和工业界的广泛关注。

DQN引入了几个关键创新:
- 经验回放(Experience Replay):存储智能体的经验(s,a,r,s’),然后随机抽样进行训练,打破样本之间的相关性
- 目标网络(Target Network):使用一个单独的网络生成目标Q值,该网络的参数定期从主网络复制,提高训练稳定性
- 卷积神经网络(CNN):处理图像输入,从原始像素中提取特征
DQN的训练过程与Q-Learning类似,但更新规则变为:
θ ← θ + α∇_θ[(r + γ·max_a’ Q(s’,a’; θ’) – Q(s,a; θ))²]
其中θ是主网络的参数,θ’是目标网络的参数。
以下是一个使用PyTorch实现DQN来玩Atari游戏(如Breakout)的代码框架:
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import random
from collections import deque
import gym
from gym.wrappers import FrameStack, GrayScaleObservation, ResizeObservation
import matplotlib.pyplot as plt
# 图像预处理
def preprocess_frame(frame):
# 转为灰度图
frame = frame.mean(axis=2)
# 调整大小为84x84
frame = frame[::2, ::2]
# 归一化
frame = frame / 255.0
return frame
# DQN网络模型
class DQN(nn.Module):
def __init__(self, input_shape, n_actions):
super(DQN, self).__init__()
self.conv = nn.Sequential(
nn.Conv2d(input_shape[0], 32, kernel_size=8, stride=4),
nn.ReLU(),
nn.Conv2d(32, 64, kernel_size=4, stride=2),
nn.ReLU(),
nn.Conv2d(64, 64, kernel_size=3, stride=1),
nn.ReLU()
)
conv_out_size = self._get_conv_out(input_shape)
self.fc = nn.Sequential(
nn.Linear(conv_out_size, 512),
nn.ReLU(),
nn.Linear(512, n_actions)
)
def _get_conv_out(self, shape):
o = self.conv(torch.zeros(1, *shape))
return int(np.prod(o.size()))
def forward(self, x):
conv_out = self.conv(x).view(x.size()[0], -1)
return self.fc(conv_out)
# 经验回放缓冲区
class ReplayBuffer:
def __init__(self, capacity):
self.buffer = deque(maxlen=capacity)
def add(self, state, action, reward, next_state, done):
self.buffer.append((state, action, reward, next_state, done))
def sample(self, batch_size):
return random.sample(self.buffer, batch_size)
def __len__(self):
return len(self.buffer)
# DQN智能体
class DQNAgent:
def __init__(self, state_shape, n_actions, device="cpu"):
self.state_shape = state_shape
self.n_actions = n_actions
self.device = device
# 创建Q网络
self.policy_net = DQN(state_shape, n_actions).to(device)
self.target_net = DQN(state_shape, n_actions).to(device)
self.target_net.load_state_dict(self.policy_net.state_dict())
self.target_net.eval()
self.optimizer = optim.Adam(self.policy_net.parameters(), lr=0.00025)
self.loss_fn = nn.MSELoss()
# 经验回放
self.replay_buffer = ReplayBuffer(100000)
# 超参数
self.gamma = 0.99
self.epsilon = 1.0
self.epsilon_decay = 0.99995
self.epsilon_min = 0.1
self.batch_size = 32
self.update_target_every = 10000
self.train_count = 0
def act(self, state):
if random.random() < self.epsilon:
return random.randrange(self.n_actions)
state = torch.FloatTensor(state).unsqueeze(0).to(self.device)
with torch.no_grad():
q_values = self.policy_net(state)
return q_values.argmax().item()
def train(self):
if len(self.replay_buffer) < self.batch_size:
return
# 从经验回放中采样
batch = self.replay_buffer.sample(self.batch_size)
states, actions, rewards, next_states, dones = zip(*batch)
states = torch.FloatTensor(states).to(self.device)
actions = torch.LongTensor(actions).unsqueeze(1).to(self.device)
rewards = torch.FloatTensor(rewards).unsqueeze(1).to(self.device)
next_states = torch.FloatTensor(next_states).to(self.device)
dones = torch.FloatTensor(dones).unsqueeze(1).to(self.device)
# 计算当前Q值
current_q = self.policy_net(states).gather(1, actions)
# 计算目标Q值
with torch.no_grad():
max_next_q = self.target_net(next_states).max(1)[0].unsqueeze(1)
target_q = rewards + (1 - dones) * self.gamma * max_next_q
# 计算损失
loss = self.loss_fn(current_q, target_q)
# 优化
self.optimizer.zero_grad()
loss.backward()
# 梯度裁剪,防止梯度爆炸
for param in self.policy_net.parameters():
param.grad.data.clamp_(-1, 1)
self.optimizer.step()
# 更新目标网络
self.train_count += 1
if self.train_count % self.update_target_every == 0:
self.target_net.load_state_dict(self.policy_net.state_dict())
# 衰减探索率
self.epsilon = max(self.epsilon_min, self.epsilon * self.epsilon_decay)
# 训练函数
def train_dqn_atari(env_name, num_frames):
# 创建环境
env = gym.make(env_name)
env = ResizeObservation(env, 84)
env = GrayScaleObservation(env)
env = FrameStack(env, 4)
state_shape = (4, 84, 84) # 4帧堆叠,每帧84x84
n_actions = env.action_space.n
# 创建智能体
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
agent = DQNAgent(state_shape, n_actions, device)
# 训练参数
rewards_history = []
best_avg_reward = -float('inf')
frame_idx = 0
while frame_idx < num_frames:
state = env.reset()
episode_reward = 0
done = False
while not done and frame_idx < num_frames:
# 选择动作
action = agent.act(state)
# 执行动作
next_state, reward, done, _ = env.step(action)
# 存储经验
agent.replay_buffer.add(state, action, reward, next_state, done)
# 训练
agent.train()
# 更新状态和奖励
state = next_state
episode_reward += reward
frame_idx += 1
# 打印进度
if frame_idx % 10000 == 0:
print(f"Frame {frame_idx}/{num_frames}, Epsilon: {agent.epsilon:.4f}")
# 记录每个回合的奖励
rewards_history.append(episode_reward)
# 计算平均奖励
avg_reward = np.mean(rewards_history[-100:])
# 打印每个回合的信息
print(f"Episode {len(rewards_history)}, Reward: {episode_reward:.2f}, Avg Reward: {avg_reward:.2f}")
# 保存表现最好的模型
if avg_reward > best_avg_reward:
best_avg_reward = avg_reward
torch.save(agent.policy_net.state_dict(), f"{env_name}_best.pth")
return agent, rewards_history
# 可视化训练结果
def plot_rewards(rewards, window_size=100):
plt.figure(figsize=(12, 8))
plt.plot(rewards)
# 绘制滑动平均线
if len(rewards) >= window_size:
avg_rewards = [np.mean(rewards[i:i+window_size]) for i in range(len(rewards)-window_size+1)]
plt.plot(range(window_size-1, len(rewards)), avg_rewards, 'r')
plt.title('训练奖励')
plt.xlabel('回合')
plt.ylabel('总奖励')
plt.grid(True)
plt.savefig('dqn_rewards.png')
plt.show()
# 测试函数
def test_dqn_atari(env_name, model_path, num_episodes=10, render=True):
# 创建环境
env = gym.make(env_name, render_mode='human' if render else None)
env = ResizeObservation(env, 84)
env = GrayScaleObservation(env)
env = FrameStack(env, 4)
state_shape = (4, 84, 84)
n_actions = env.action_space.n
# 加载模型
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = DQN(state_shape, n_actions).to(device)
model.load_state_dict(torch.load(model_path, map_location=device))
model.eval()
# 测试
total_rewards = []
for episode in range(num_episodes):
state = env.reset()
episode_reward = 0
done = False
while not done:
# 选择动作
state_tensor = torch.FloatTensor(state).unsqueeze(0).to(device)
with torch.no_grad():
q_values = model(state_tensor)
action = q_values.argmax().item()
# 执行动作
next_state, reward, done, _ = env.step(action)
# 更新状态和奖励
state = next_state
episode_reward += reward
if render:
env.render()
total_rewards.append(episode_reward)
print(f"Episode {episode+1}/{num_episodes}, Reward: {episode_reward:.2f}")
env.close()
print(f"Average Reward: {np.mean(total_rewards):.2f}")
# 主函数
if __name__ == "__main__":
env_name = "BreakoutNoFrameskip-v4"
num_frames = 1000000 # 1M帧,实际训练可能需要10M帧以上
# 训练
agent, rewards = train_dqn_atari(env_name, num_frames)
plot_rewards(rewards)
# 测试
test_dqn_atari(env_name, f"{env_name}_best.pth")
实现DQN最困难的部分是处理稳定性问题。在早期版本中,Q值会发散或者智能体陷入次优策略。DeepMind后续提出了许多改进,如Double DQN、Dueling DQN和Prioritized Experience Replay等,进一步提高了性能和稳定性。
从离散到连续:强化学习的动作空间探索
到目前为止,我们讨论的例子都是离散动作空间,比如在迷宫中选择上下左右移动,或者在Atari游戏中选择几个预定义的按钮。但真实世界的许多问题涉及连续动作空间,比如机器人控制中的关节角度或力量控制。
在连续动作空间中,我们不能简单地列举所有可能的动作并选择Q值最大的那个。因此,需要不同的算法,如策略梯度(Policy Gradient)、DDPG(Deep Deterministic Policy Gradient)或PPO(Proximal Policy Optimization)。
这些算法不再学习Q值,而是直接学习一个策略函数π(a|s),表示在状态s下采取动作a的概率分布。训练目标是最大化期望回报。
实际应用与未来展望
强化学习已经在许多领域展现出惊人的能力:
- 游戏AI:从象棋、围棋到星际争霸,强化学习算法已经达到或超过人类水平
- 机器人控制:帮助机器人学习行走、抓取物体等复杂任务
- 推荐系统:优化用户体验和长期参与度
- 能源管理:优化数据中心冷却系统,减少能源消耗
- 自动驾驶:学习复杂的驾驶策略
未来,随着算法的改进和计算能力的提升,强化学习有望解决更多复杂问题。特别是结合大型语言模型和多模态感知,强化学习可能会为通用人工智能铺平道路。
回到起点:迷宫与思考
记得我一开始提到的那个简单迷宫游戏吗?现在回过头来看,它其实包含了强化学习的所有核心元素:状态、动作、奖励、探索与利用的平衡,以及学习最优策略的过程。
当我看到我的机器人智能体从最初的随机游走,逐渐学会避开障碍物,最终找到通往目标的最短路径时,那种成就感是无法言喻的。这种从无到有的学习能力,正是强化学习最迷人的地方。
强化学习的美妙之处在于,它不仅是一种算法,更是一种思考问题的方式。它教会我们如何在不确定性中做决策,如何平衡短期与长期利益,以及如何通过不断尝试来改进。这些原则不仅适用于AI,也适用于我们的日常生活。
所以,无论你是对AI感兴趣的初学者,还是寻找解决复杂决策问题的专业人士,强化学习都值得你深入探索。它可能会改变你看待问题和解决问题的方式,就像它改变了我的视角一样。
让我们像智能体一样,在这个充满不确定性的世界中,勇敢探索,从错误中学习,不断优化我们的"策略",追求最大的长期"奖励"。
"试错、学习、优化——强化学习的精髓,或许也是人生的真谛。"