想象一下,你在一个浓雾弥漫的山谷中迷路了,手里只有一个指南针,目标是找到海拔最低的地方。你会怎么做?最自然的想法就是感受脚下地面的倾斜,朝着最陡峭的下坡方向走,一步一步地接近谷底。这个朴素而直观的想法,竟然成就了现代人工智能最重要的优化算法之一——梯度下降。
网页版:https://uhluenaw.gensparkspace.com
视频版:https://www.youtube.com/watch?v=C542vqkYzew
音频版:https://notebooklm.google.com/notebook/69f3cc1c-b42d-43fc-8fa6-0abac4b39693/audio
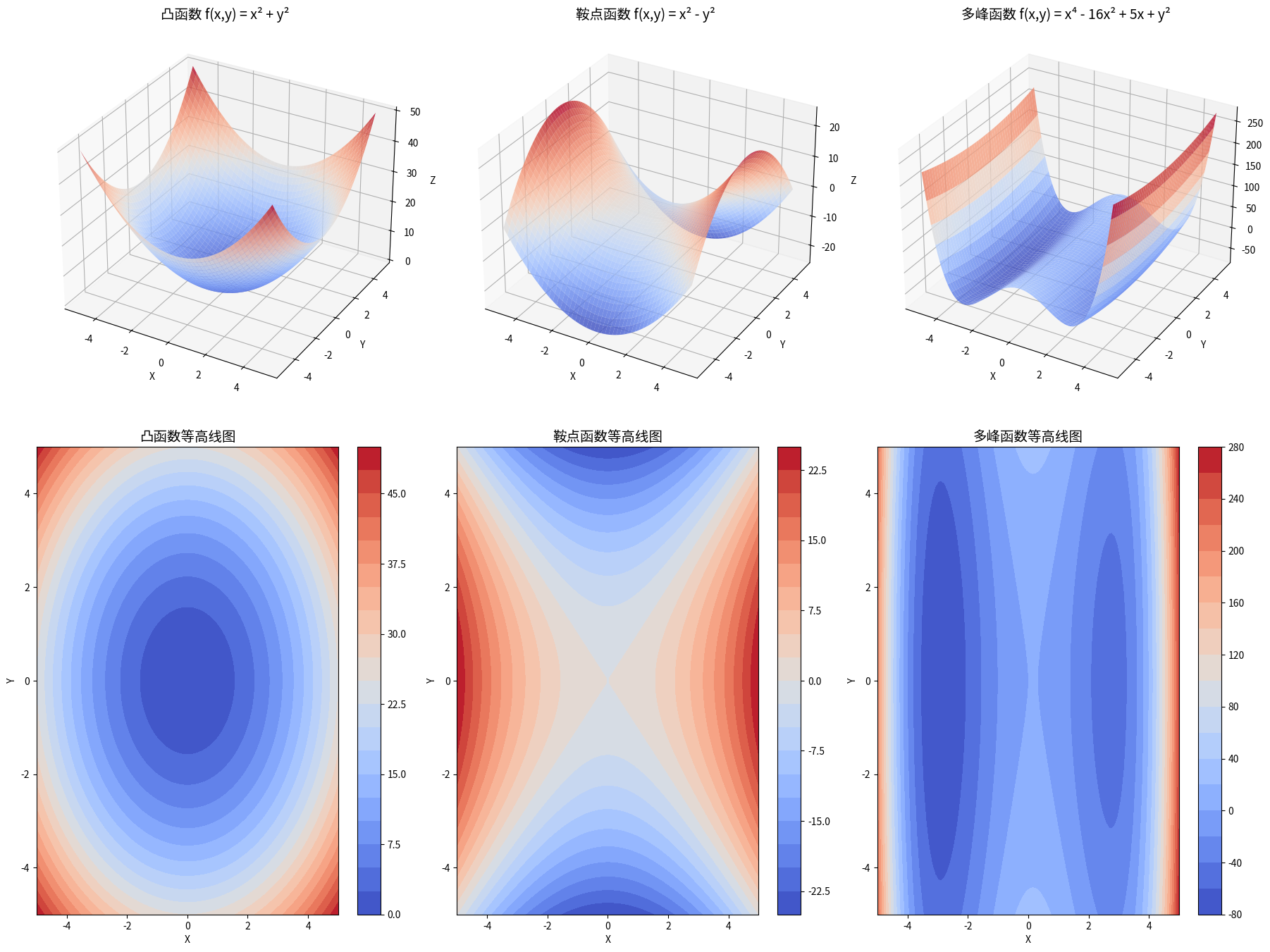
数学的直觉:从一维到多维的奇妙扩展
在高中时代,我们都学过求导数来找函数的最小值点。但现实世界的问题往往涉及成千上万个变量,这时候普通的导数就显得力不从心了。偏导数的概念应运而生,它告诉我们在多维空间中如何沿着某一个方向"窥探"函数的变化趋势。
更有趣的是梯度的概念。如果说偏导数是一个个单独的"探头",那么梯度就像是一个全方位的"雷达",它能精确地指出函数在任意一点增长最快的方向。Machine Learning Mastery的这篇文章用生动的例子解释了这个概念。
想想地形图上的等高线,当你站在某个位置时,梯度矢量永远垂直于通过这一点的等高线,指向海拔上升最快的方向。而梯度下降算法做的事情恰恰相反——它沿着梯度的反方向前进,也就是下降最快的方向。
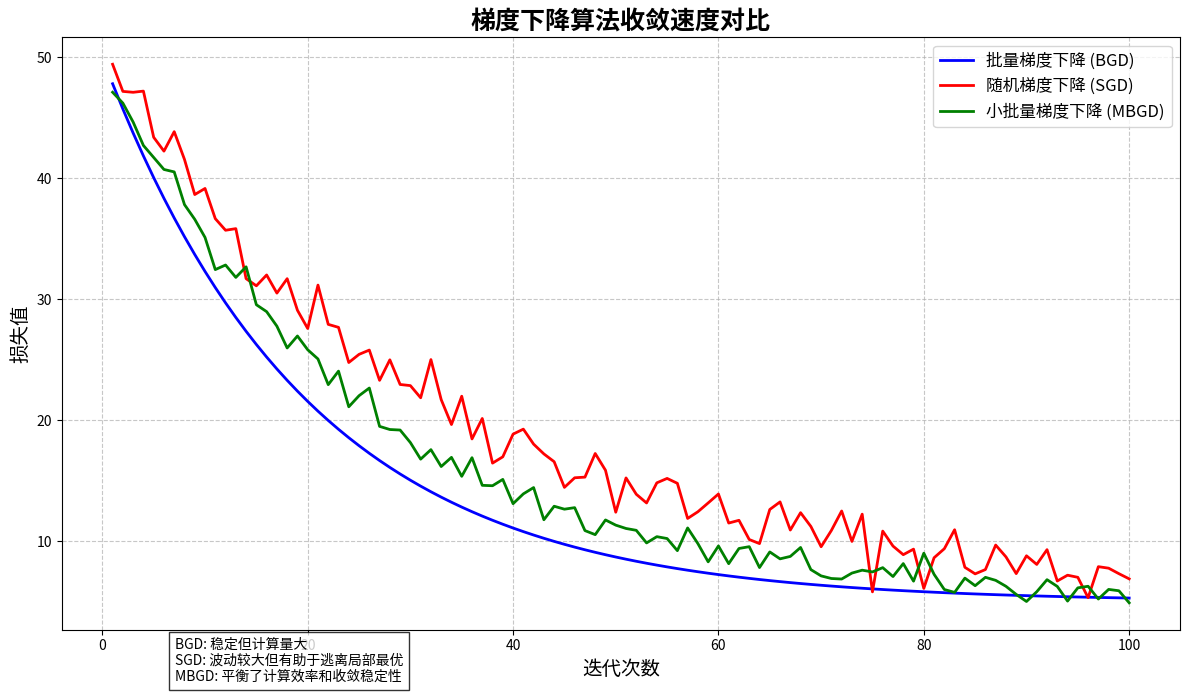
三兄弟的不同性格:BGD、SGD和MBGD
在梯度下降这个大家族中,有三个性格迥异的兄弟。老大BGD(Batch Gradient Descent)性格稳重,做事周全。他每次都要把所有数据看一遍才敢迈出一步,虽然路线最稳,但速度确实不快。这个实现教程详细展示了BGD的工作方式。
老二SGD(Stochastic Gradient Descent)就像个急性子,看一个数据点就立刻行动。虽然路线看起来摇摇摆摆,但正是这种"随机性"让他有机会逃离局部最优的陷阱,在大数据时代大放异彩。
老三MBGD(Mini-Batch Gradient Descent)集合了两个哥哥的优点,每次看一小批数据再行动,既保持了一定的稳定性,又提高了计算效率,成为了实际应用中最受欢迎的算法。
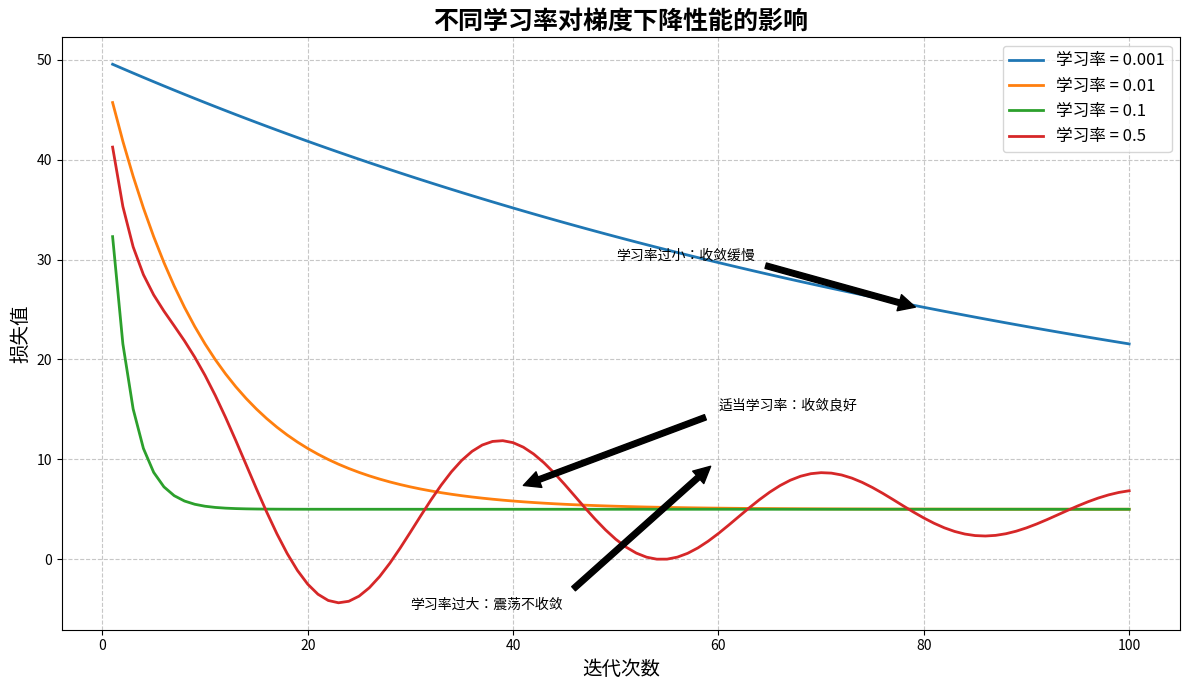
学习率:算法的"步伐大小"
学习率就像是算法的"步伐大小"。步子太小,就像蹒跚学步的婴儿,虽然稳当但到达目的地需要很长时间。步子太大,就像冲动的青少年,容易在目标附近来回摇摆,永远无法精确到达。只有恰当的步伐,才能既快速又稳定地抵达目标。
有趣的是,在优化的过程中,算法会遇到各种"地形":有些地方是平缓的山坡(凸函数),有些地方是马鞍形的山脊(鞍点),还有些地方是起伏不定的丘陵(多峰函数)。不同的地形需要不同的"走法"。
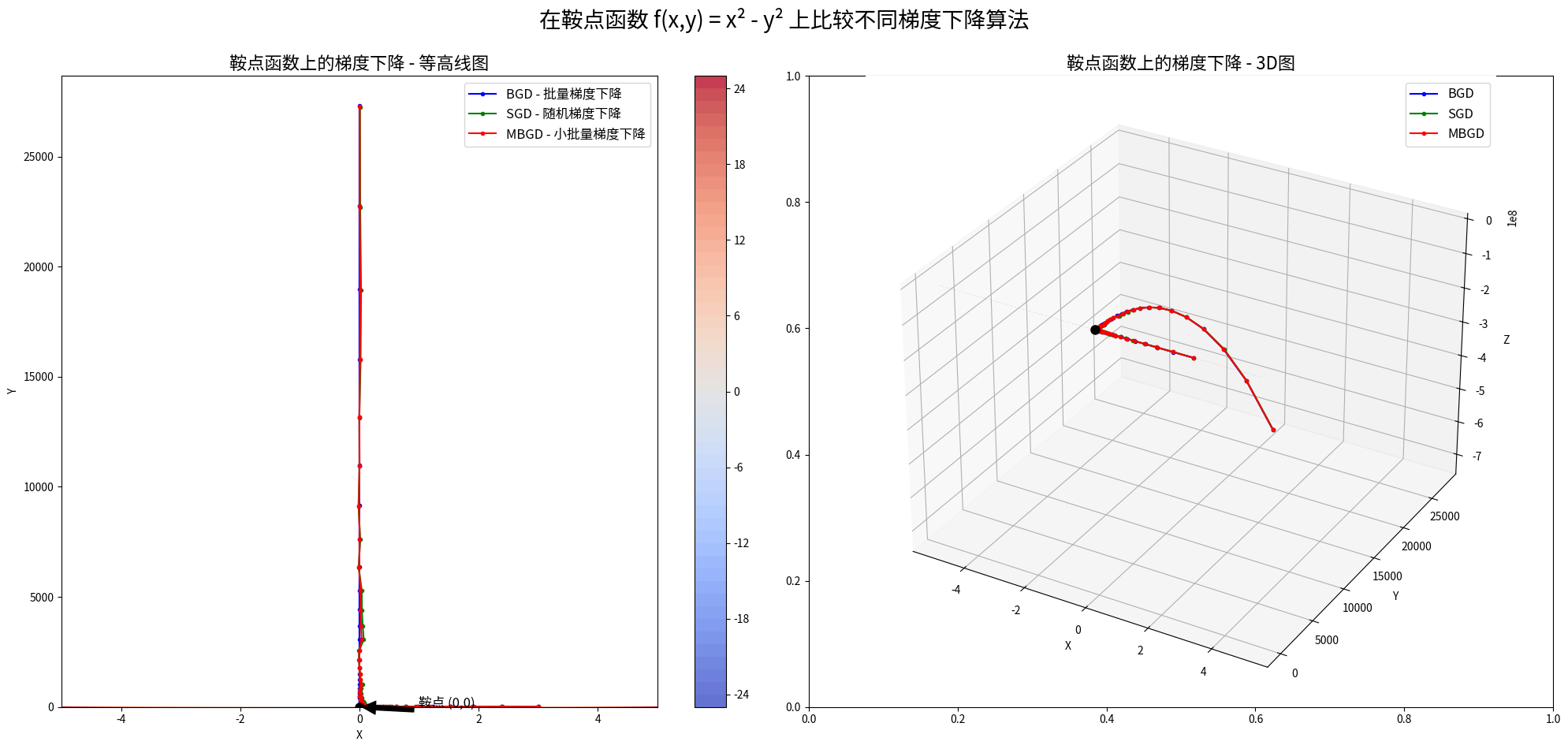
鞍点的挑战:数学中的"悬崖勒马"
鞍点是优化中的一个有趣现象。想象你骑马走到了一个山脊上,左右是深谷,前后是山坡。这就是鞍点——在某些方向上是最小值,在另些方向上却是最大值。Khan Academy对鞍点的解释非常直观。
现代深度学习研究发现,高维空间中的鞍点数量远多于局部最小值。这意味着大多数时候,算法"卡住"的地方并不是真正的局部最优,而是鞍点。理解这一点让研究者们对深度学习的成功有了新的认识。
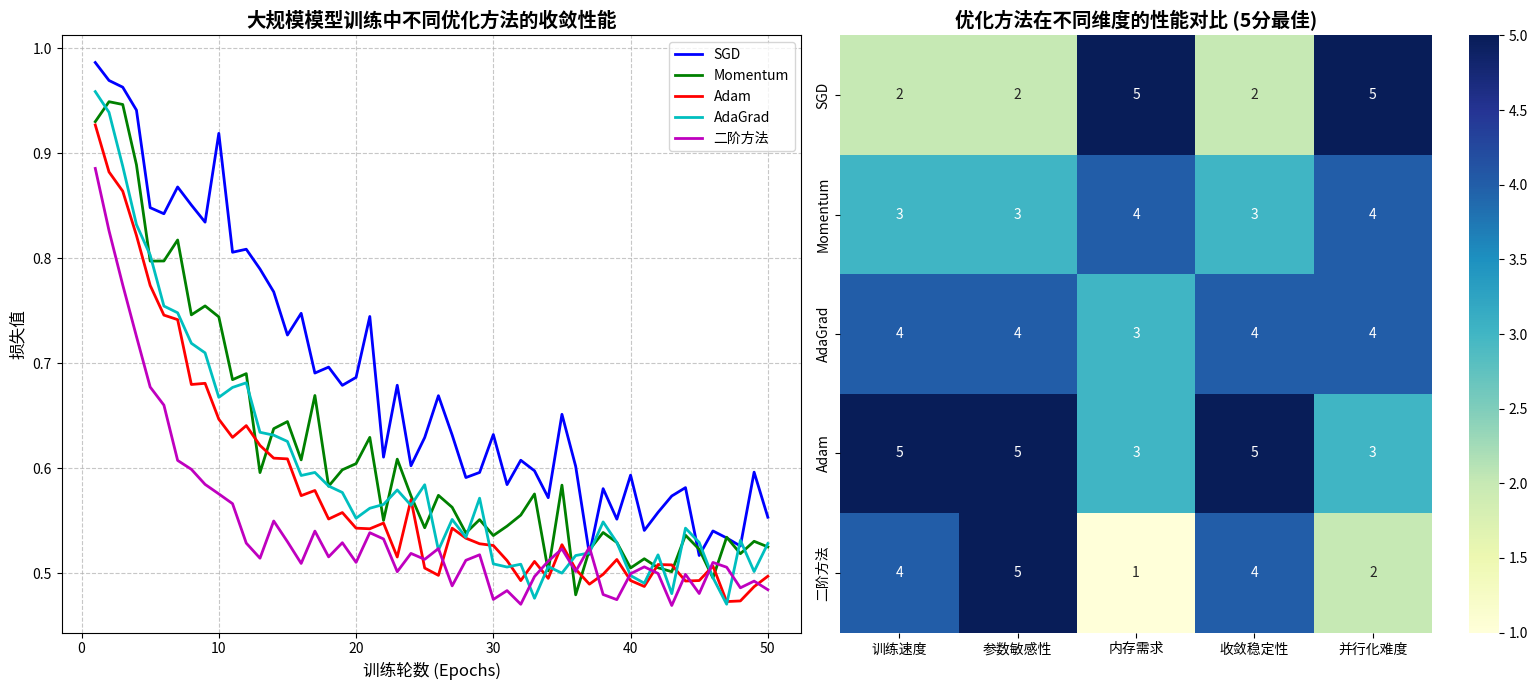
现代优化:从简单到复杂的演进
随着机器学习模型变得越来越复杂,简单的梯度下降已经不能满足需求。就像汽车从手摇启动进化到电子点火,优化算法也在不断进化。
Momentum算法就像给小球加了惯性,即使遇到小的上坡也能冲过去。Adam算法更聪明,它会根据历史信息自动调整每个参数的学习率。这篇关于现代优化器的综述详细介绍了这些算法的发展历程。
在大规模模型训练中,研究者们开发了ZeRO、梯度累积等技术,让我们能够训练拥有千亿参数的大型语言模型。
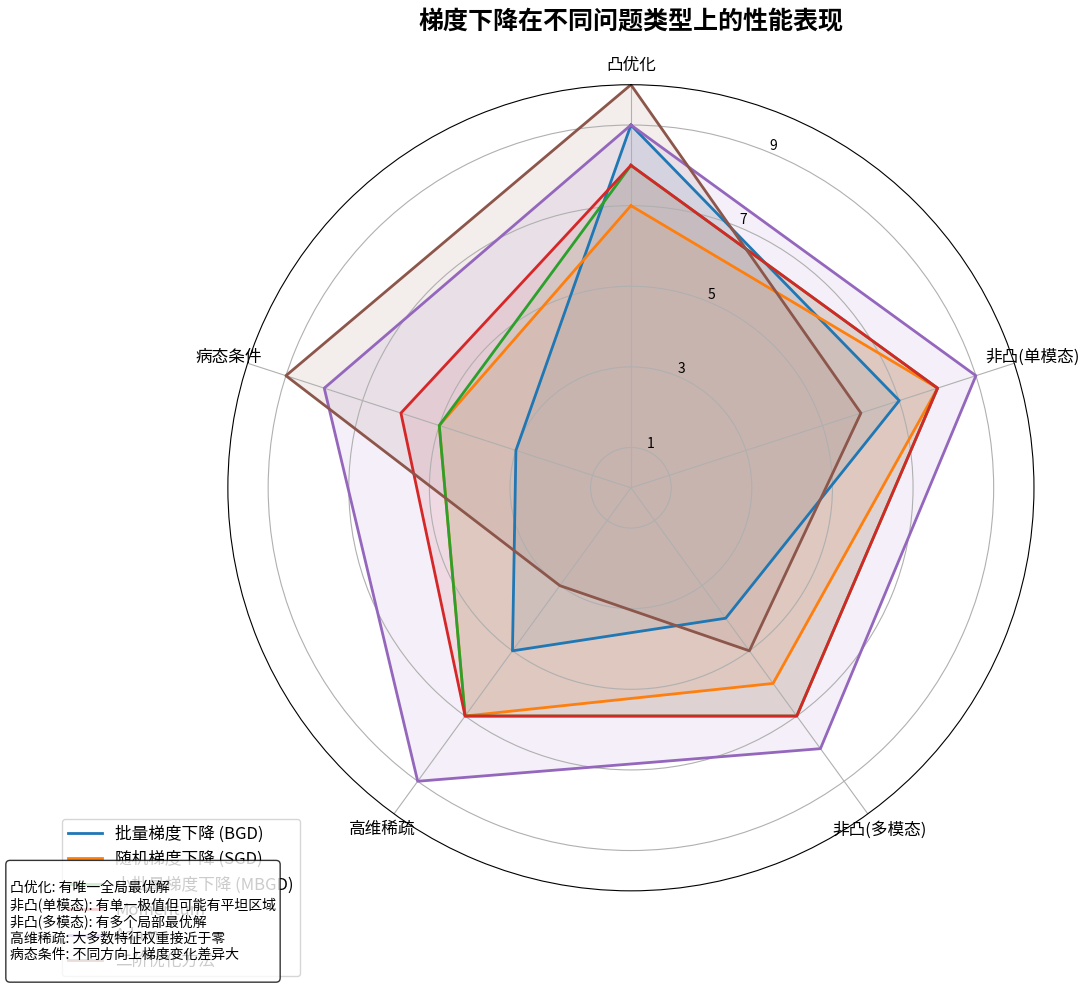
约束中的优美:拉格朗日乘数法
有时候,优化问题不是在整个空间中自由寻找最优解,而是要在某些约束条件下进行。就像在一个圆形池塘里找最深的点,你不能随便往外走,必须待在池塘里。
拉格朗日乘数法提供了一个优雅的解决方案。它的核心思想是:在最优点处,目标函数的梯度必须与约束条件的梯度平行。这个看似简单的几何直觉,却能解决复杂的约束优化问题。Paul’s Online Math Notes提供了详细的推导过程。
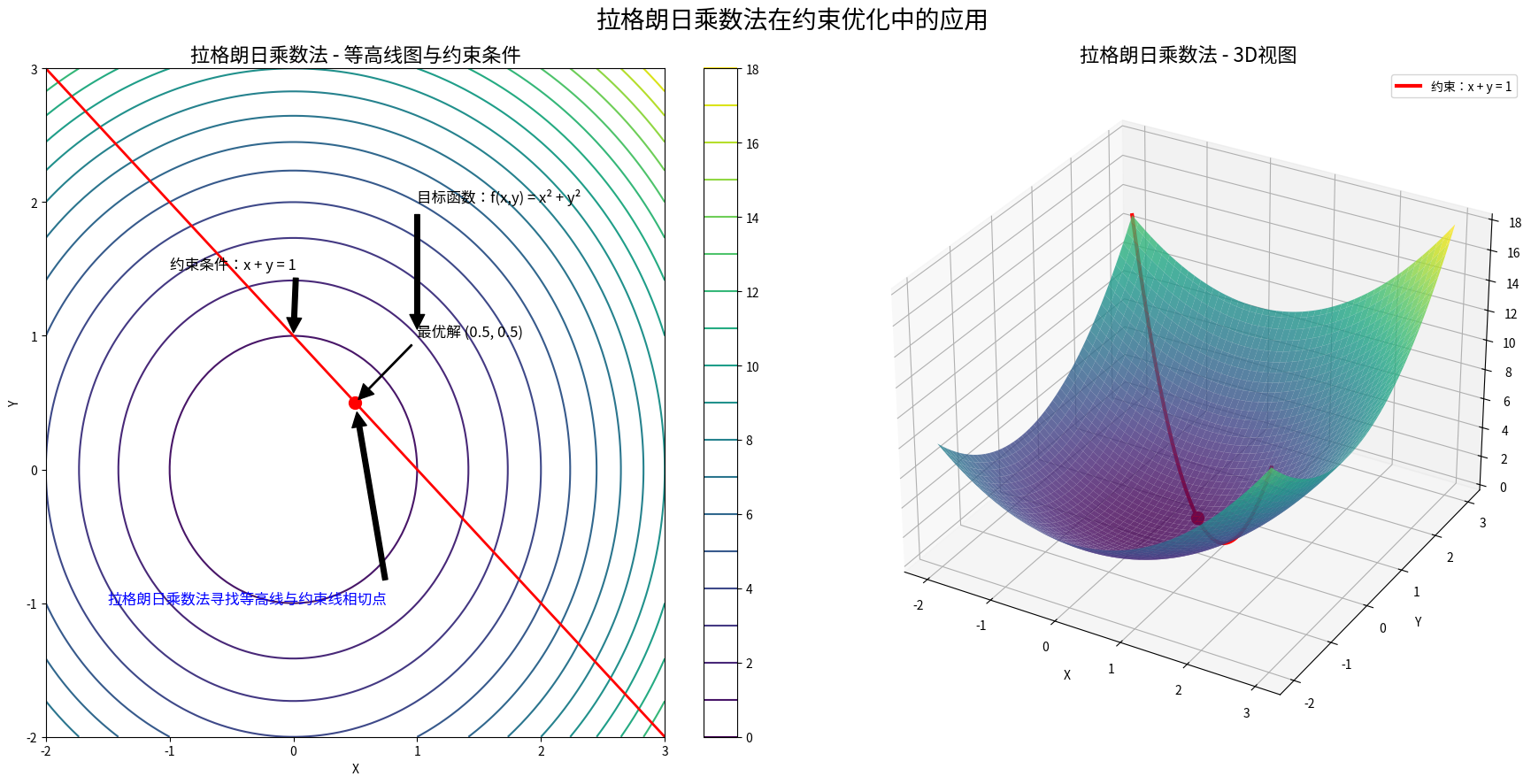
链式法则:复合函数的"传话游戏"
现代深度学习的成功很大程度上归功于反向传播算法,而反向传播的数学基础就是链式法则。想象一个传话游戏:信息从输入层一层层传到输出层,然后误差信号又从输出层一层层传回输入层。每一层的传递都要用到链式法则。
在深度神经网络中,一个小小的输入变化会如何影响最终的输出?链式法则告诉我们答案。这就像多米诺骨牌效应,每一层的变化都会影响下一层,最终影响到整个网络的输出。
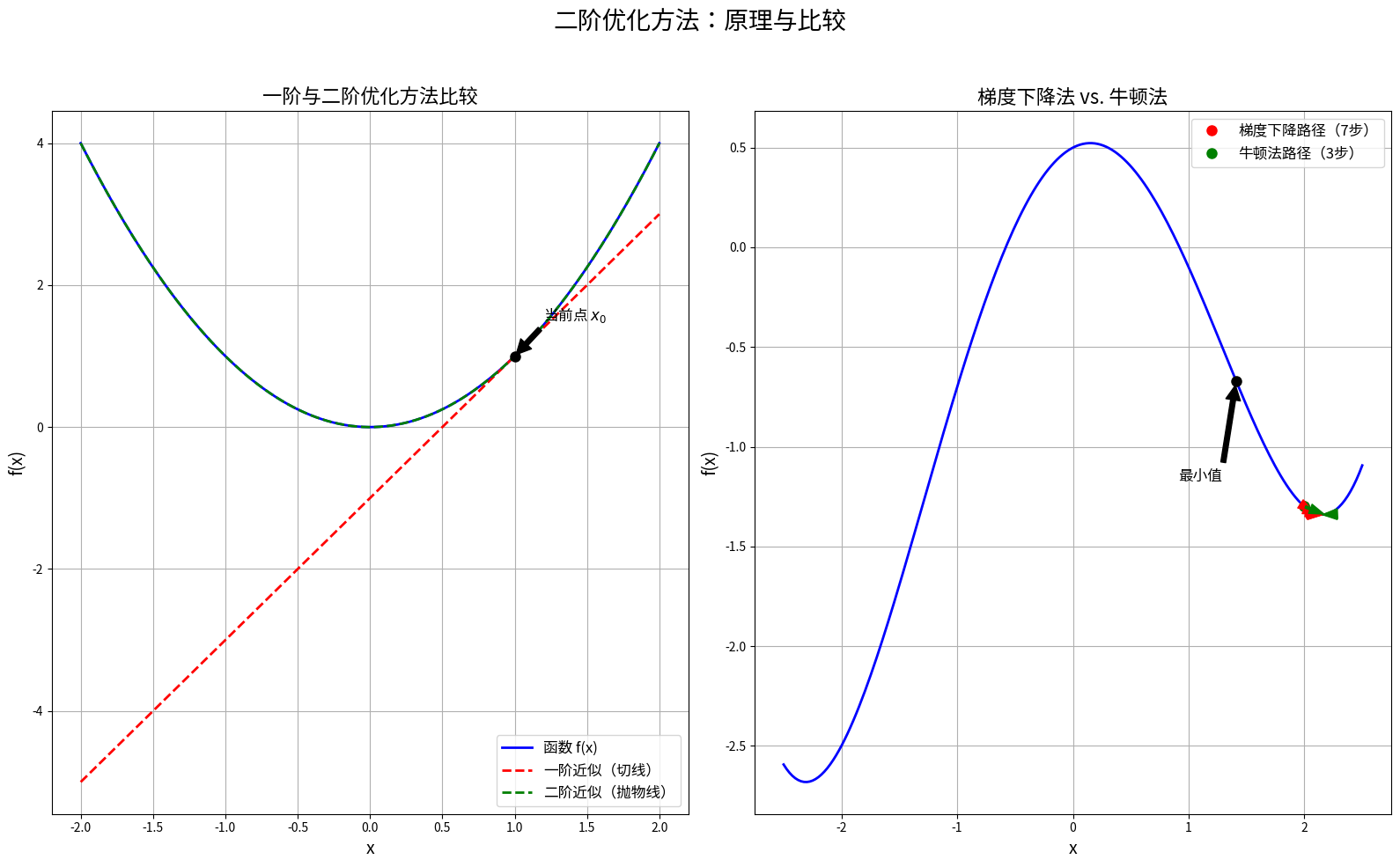
二阶方法:优化的"透视眼"
如果说一阶方法(梯度下降)只能看到函数的"坡度",那么二阶方法就像有了"透视眼",能看到函数的"弯曲程度"。牛顿法就是典型的二阶方法,它利用函数的二阶导数信息(Hessian矩阵)来选择更好的前进方向。
虽然二阶方法通常收敛更快,但计算和存储二阶导数的代价在高维空间中变得非常昂贵。这就像开法拉利跑车,性能确实好,但油耗也确实高。因此,研究者们开发了拟牛顿法等折中方案,试图在计算效率和收敛速度之间找到平衡。
实践中的智慧:算法选择的艺术
选择合适的优化算法就像选择合适的交通工具。在平坦的高速公路上,你可能更愿意开快车;在崎岖的山路上,你可能需要一辆越野车;在拥堵的城市中,也许自行车更实用。
在凸优化问题中,传统的梯度下降方法通常表现良好。在非凸问题中,SGD的随机性可能帮助算法逃离局部最优。在高维稀疏问题中,Adam等自适应算法往往表现更好。在大规模分布式训练中,LAMB等专门设计的算法可能是更好的选择。
未来的展望:优化算法的新边疆
优化算法的发展永远不会停止。研究者们正在探索量子优化、进化算法、神经网络架构搜索等新方向。每一个突破都可能为人工智能带来新的飞跃。
就像当年牛顿通过研究苹果落地发现了万有引力定律,今天的研究者们通过研究优化算法,也在不断揭示学习和智能的本质。从简单的梯度下降,到复杂的自适应优化器,每一个算法都承载着人类对于"如何更好地学习"这个根本问题的思考。
这场从数学公式到智能应用的奇妙旅程还在继续。无论是在实验室里推导新的理论,还是在数据中心里训练大型模型,优化算法都是连接数学之美与现实应用的重要桥梁。正如著名数学家欧拉所说:"数学是上帝用来书写宇宙的语言",而优化算法,或许就是我们学会阅读这种语言的方式。