想象一下,你正站在一个充满神秘色彩的数字世界门口。这里有两位引路人,一位是睿智的贝叶斯先生,他总是在脑海中快速计算着各种可能性;另一位是朴实的邻居K君,他相信"物以类聚,人以群分"的古老智慧。今天,我们将跟随这两位向导,踏上一段关于机器学习的奇妙探索之旅。
网页版:https://www.genspark.ai/api/page_private?id=pqpgokdu
视频版:https://www.youtube.com/watch?v=R_ec2XXHWy8
音频版:https://notebooklm.google.com/notebook/93bf5e35-6a63-466b-a790-9d37173e1364/audio
在这个故事的开头,让我先为你描绘一幅画面。你收到了一封来历不明的邮件,标题写着"恭喜中奖!立即领取一千万大奖!"这时候,你的大脑会自动开始一个复杂的判断过程——这是贝叶斯先生在悄悄工作。他会综合考虑这封邮件的各种特征:发件人地址、用词习惯、语法错误,然后基于你过往的经验,给出一个概率判断:"这是垃圾邮件的可能性是95%"。
这正是朴素贝叶斯分类器的工作原理。它像一个经验丰富的侦探,通过观察证据(特征)来推断真相(分类)。根据GeeksforGeeks的研究,这个算法基于一个看似简单却威力巨大的数学公式——贝叶斯定理。

贝叶斯定理:概率世界的黄金法则
贝叶斯定理就像是概率世界的"黄金法则",它告诉我们如何在获得新信息后更新我们的信念。用数学语言表达就是:
P(A|B) = P(B|A) × P(A) / P(B)
这个公式看起来可能有些抽象,但让我用一个生动的例子来解释。假设你是一位医生,正在诊断一个患者是否患有某种罕见疾病。根据斯坦福大学的研究,即使某个测试的准确率高达99%,但如果这种疾病的患病率只有0.1%,那么一个阳性结果实际表示患病的概率可能只有9%左右。这就是贝叶斯定理在现实世界中的威力体现。

朴素贝叶斯之所以被称为"朴素",是因为它做了一个大胆的假设:所有特征之间都是条件独立的。就像评判一个人的品格时,我们假设他的善良和智慧是独立的品质。虽然现实中这种完全独立很少存在,但正如DataCamp的分析显示,这个"朴素"的假设往往能带来出人意料的好结果。
拉普拉斯平滑:优雅地处理未知
在机器学习的世界里,总会遇到一些前所未见的情况。想象你正在训练一个垃圾邮件分类器,突然遇到了一个包含全新词汇的邮件。如果按照简单的概率计算,这个词汇的出现概率为零,整个分类结果就会变成零——这显然不合理。
这时候,拉普拉斯平滑就像一位温和的调解者登场了。根据Towards Data Science的深入解析,它为每个特征添加一个小的常数(通常是1),确保没有任何概率为零。这种方法既保持了数学的严谨性,又体现了对未知情况的包容态度。
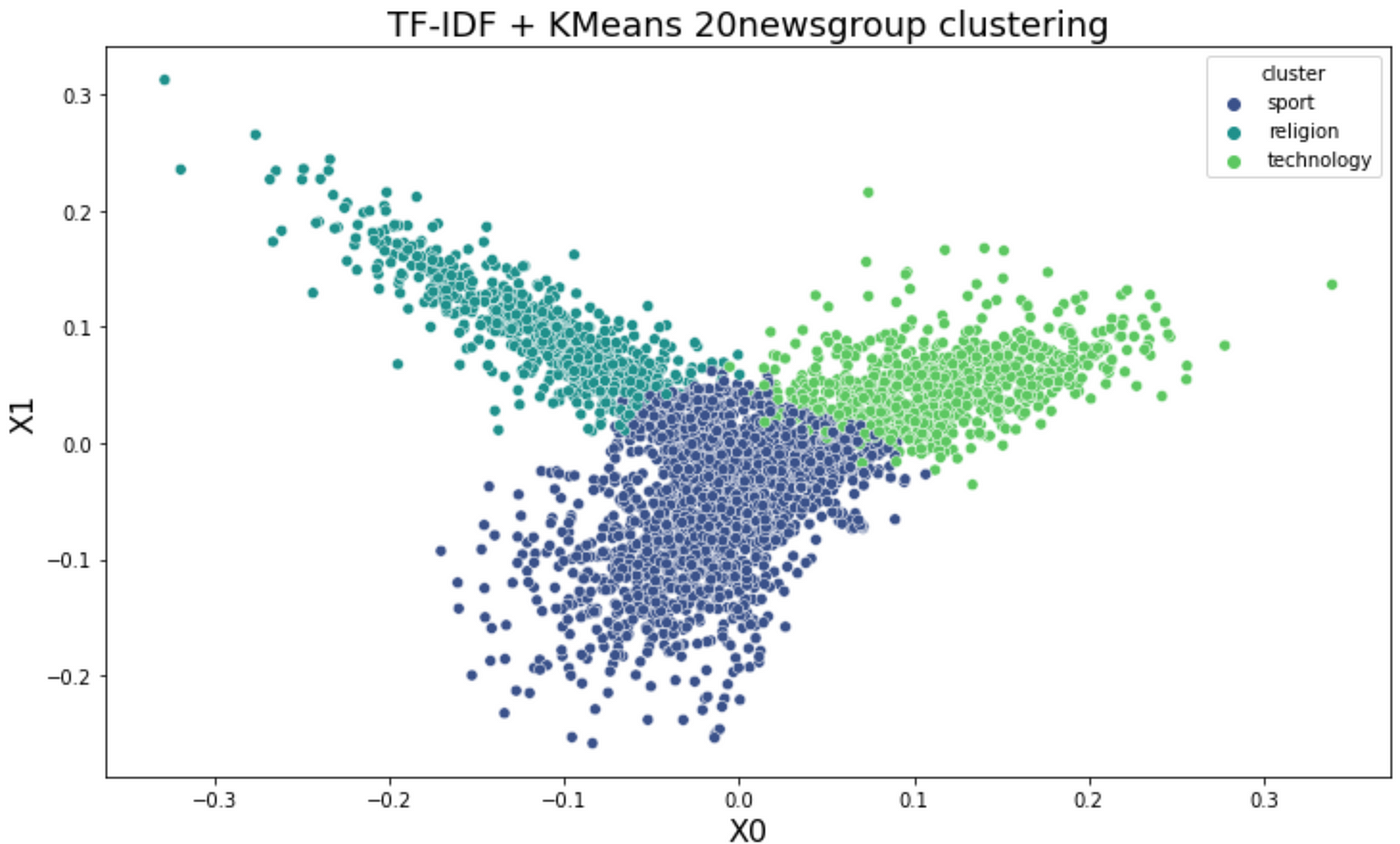
在文本分类任务中,朴素贝叶斯经常与TF-IDF特征提取技术结合使用。TF-IDF就像是文本世界的"重要性指标",它不仅考虑一个词在文档中出现的频率,还考虑这个词在整个语料库中的稀有程度。正如Enigma的技术分析所示,这种组合在新闻分类、情感分析等任务中表现出色。
K近邻:简单却深刻的哲学
如果说朴素贝叶斯是一位数学家,那么K近邻(KNN)就像是一位人类学家。它相信一个朴素而深刻的道理:"告诉我你的朋友是谁,我就知道你是什么样的人。"
K近邻算法的工作方式极其直观。面对一个新的数据点,它会在训练数据中寻找K个最相似的"邻居",然后通过这些邻居的"投票"来决定新数据点的类别。PyImageSearch的详细教程生动地展示了这个过程:在一个由猫、狗、熊猫组成的图像分类任务中,KNN通过比较像素相似度来判断一张新图片最可能属于哪个类别。

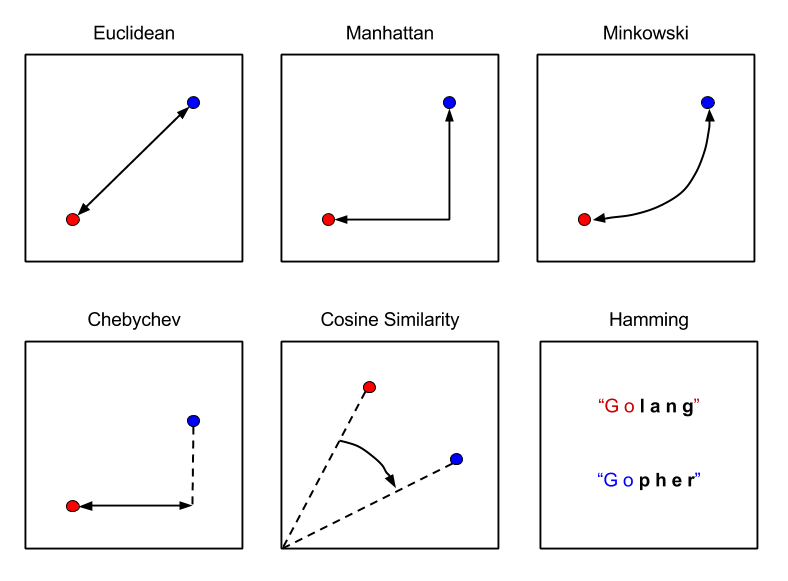
KNN的魅力在于其多样的距离度量方式。欧氏距离就像是我们日常生活中的直线距离,适合大多数连续数值特征;曼哈顿距离则像城市中的出租车路线,在处理高维稀疏数据时更加有效;而余弦相似度关注的是方向而非大小,在文本分析中特别有用。根据KDnuggets的研究,选择合适的距离度量往往能将分类准确率提升5-15%。
K值选择:平衡的艺术
选择合适的K值就像是走钢丝的艺术。K值太小(比如K=1),算法会过度敏感,容易被噪声数据误导;K值太大,又可能过度平滑,丢失重要的局部特征。Medium上的深度分析提到,通常使用交叉验证、肘部法则等技术来寻找最优的K值。
有趣的是,KNN被称为"懒惰学习"算法,但这种"懒惰"其实蕴含着深刻的哲学。它不急于在训练阶段就做出判断,而是等到真正需要分类时才"临时抱佛脚"。这种策略使得它能够适应数据的局部变化,但也带来了计算复杂度的挑战。
kd树优化:高维空间的导航系统
当数据维度增高时,朴素的KNN算法会陷入"维度诅咒"的困境。这时候,kd树就像是高维空间中的GPS导航系统。根据GeeksforGeeks的技术解析,kd树通过递归地将数据空间划分成超矩形区域,大大减少了搜索最近邻时需要比较的数据点数量。
实战应用:从垃圾邮件到图像识别
让我们回到开头的垃圾邮件例子。现代的垃圾邮件过滤系统通常会结合朴素贝叶斯和其他算法。Kaggle上的经典案例显示,基于词频的朴素贝叶斯分类器能够达到95%以上的准确率。系统会分析邮件中"免费"、"中奖"、"点击这里"等词汇的出现频率,结合发件人信息、时间戳等特征,最终给出垃圾邮件的概率判断。
在图像识别领域,KNN虽然看似简单,但在某些场景下表现惊人。PyImageSearch的动物分类实验中,仅仅基于32×32像素的原始RGB值,KNN就能在猫、狗、熊猫的三分类任务中达到41%的准确率——虽然不算高,但考虑到随机猜测的准确率只有33%,这个结果已经相当不错了。
懒惰学习的哲学思考
KNN的"懒惰学习"特性引发了有趣的哲学思考。与神经网络等"勤奋"的算法不同,KNN选择了一种更加"禅意"的方式:不预设判断,不急于学习,而是在每次预测时都重新审视所有的训练数据。这种方法的时间复杂度是O(n),在大数据时代确实是个挑战,但它也带来了独特的优势:适应性强、对数据分布不敏感、天然支持多分类。
根据Arize AI的深度分析,虽然KNN在训练阶段几乎不消耗时间,但在预测阶段需要与所有训练数据进行比较,这种特性使得它在实时性要求高的场景中面临挑战。
计算复杂度:效率与准确性的权衡
朴素贝叶斯和KNN在计算复杂度上呈现出有趣的对比。朴素贝叶斯在训练阶段需要计算各种概率分布,但一旦训练完成,预测速度极快,时间复杂度仅为O(c×n),其中c是类别数,n是特征数。而KNN则相反,训练几乎不耗时,但每次预测都需要遍历整个训练集。
这种差异反映了机器学习中一个重要的权衡原则:你可以选择在训练时投入更多资源以换取快速预测,也可以选择快速训练但接受相对较慢的预测速度。现实应用中,这种选择往往取决于具体的业务场景和性能要求。
高维数据的挑战与机遇
在处理高维稀疏数据(如文本数据)时,两种算法展现出不同的特性。朴素贝叶斯由于其特征独立性假设,在高维文本分类任务中表现优异。scikit-learn的官方文档显示,多项式朴素贝叶斯在处理文档分类任务时,即使特征维度达到数万维,仍能保持良好的性能。
相比之下,KNN在高维空间中面临更大挑战。当维度增加时,所有点之间的距离趋于相等,最近邻的概念变得模糊不清。这就是著名的"维度诅咒"问题。但通过合适的降维技术或特征选择,KNN仍然可以在高维数据中发挥作用。
我们的探索之旅即将结束,但学习的道路永远没有终点。朴素贝叶斯教会我们用概率的眼光看世界,相信数据中蕴含的规律;KNN提醒我们不要忘记直觉的力量,有时候最简单的方法往往最有效。
在这个AI技术日新月异的时代,理解这些基础算法的原理和哲学,不仅能帮助我们更好地运用现代深度学习技术,也能在面对新问题时保持清醒的判断力。毕竟,再复杂的神经网络,其核心思想往往可以追溯到这些经典算法的智慧之中。
当你下次收到可疑邮件或需要对图像进行分类时,不妨想想贝叶斯先生的概率计算和邻居K君的投票机制。在这个充满算法的数字世界里,每一个预测背后都有着深刻的数学原理和人类智慧的结晶。