想象一下,你正站在一个复杂的迷宫入口。前方的道路错综复杂,每一步都可能通向宝藏,也可能走向死胡同。如果你拥有一张详尽的地图,知道每个转弯后会遇到什么,每条路径的奖励如何,你会如何制定最优策略?这就是动态规划在强化学习中要解决的核心问题。
视频版:https://www.youtube.com/watch?v=WC-PDYh1QLg
在人工智能的浩瀚星空中,强化学习如同一颗闪亮的明星,而动态规划则是这颗明星最核心的引擎之一。从1950年代贝尔曼提出动态规划原理开始,这个优雅的数学框架就一直在为复杂决策问题提供着精确而可靠的解决方案。
基础概念:模型驱动的智能决策
动态规划在强化学习中扮演着基石般的角色。与那些需要通过试错学习的方法不同,动态规划假设我们对环境有着完全的了解——就像拥有了那张详尽的迷宫地图。在这个"全知"的世界里,我们知道从任何状态采取任何行动后会转移到哪个新状态,以及会获得多少奖励。
这种"基于模型"的特性让动态规划具备了独特的优势。根据斯坦福大学的research,当环境模型已知时,动态规划方法能够保证找到全局最优解,这是其他许多强化学习算法无法提供的强有力保证。
贝尔曼方程:决策的数学诗篇
在深入具体算法之前,我们必须先理解贝尔曼方程——这个被誉为"强化学习中最重要方程"的数学表达式。1957年,数学家理查德·贝尔曼在研究最优控制问题时,提出了这个革命性的递归关系式。

贝尔曼方程的核心思想令人着迷:一个状态的价值等于在该状态下采取最优行动所获得的即时奖励,加上未来所有可能状态价值的期望折扣和。用数学语言表达,就是:
$$V^(s) = \max_a \sum_{s’} P(s’|s,a)[R(s,a,s’) + \gamma V^(s’)]$$
这个看似简单的方程背后蕴含着深刻的哲学思考。正如MIT的研究论文所指出的,贝尔曼方程体现了"最优子结构"的重要性质:最优策略的任何子策略也必须是相应子问题的最优策略。
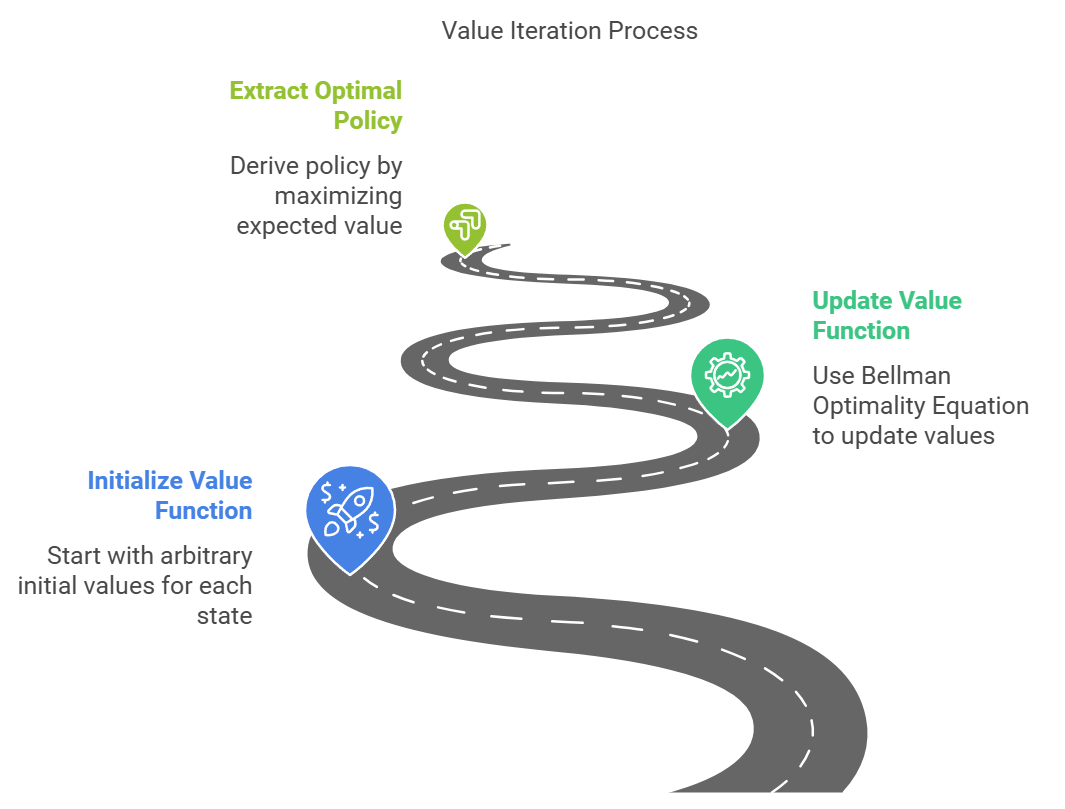
价值迭代:逐步逼近完美的艺术
价值迭代算法是动态规划家族中最直观的成员。它的工作原理如同艺术家精雕细琢一件作品,每一次迭代都让我们更接近完美的解决方案。

算法的核心流程包含四个步骤,形成了一个优雅的循环:
- 初始化:为所有状态设置初始价值(通常为零)
- 价值更新:使用贝尔曼方程更新每个状态的价值
- 收敛检测:检查价值函数的变化是否足够小
- 策略提取:从最终的价值函数中提取最优策略
David Silver在其强化学习课程中强调,价值迭代的美妙之处在于其收敛性保证。由于贝尔曼算子是一个压缩映射,价值迭代必然收敛到唯一的最优价值函数。这种数学上的严格性让价值迭代成为了理论研究的重要工具。
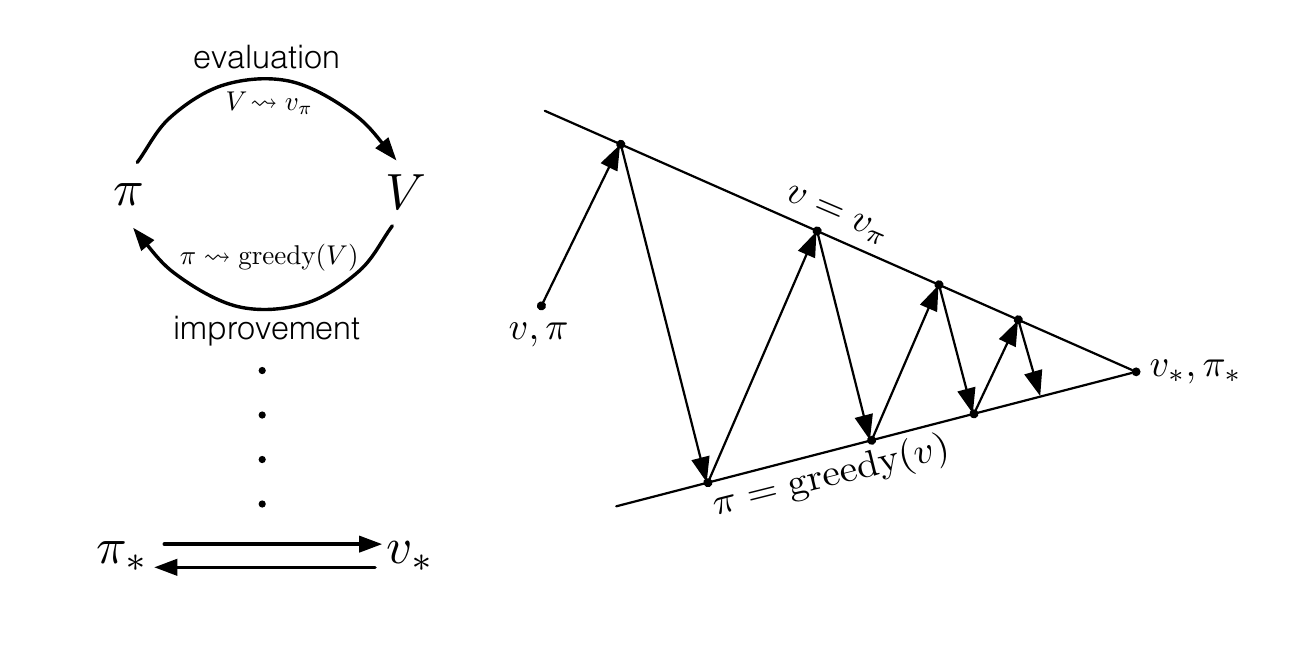
策略迭代:双重奏的智慧
如果说价值迭代是独奏者的精彩演出,那么策略迭代就是双重奏的和谐协作。这个算法巧妙地将问题分解为两个交替进行的过程:策略评估和策略改进。
策略评估阶段专注于计算当前策略下每个状态的价值。这个过程如同一个会计师仔细核算每个决策的收益。通过反复应用贝尔曼期望方程,我们可以精确计算出给定策略的价值函数:
$$V^\pi(s) = \sum_a \pi(a|s) \sum_{s’} P(s’|s,a)[R(s,a,s’) + \gamma V^\pi(s’)]$$
策略改进阶段则像一个智慧的优化师,根据当前的价值函数,为每个状态选择能带来最大价值的行动。这个贪婪改进过程保证了新策略不会比原策略差,通常还会带来显著的改进。
根据Sutton和Barto的经典教材,策略迭代的理论优势在于其策略改进定理的保证。这个定理表明,如果存在任何状态的价值可以通过改变策略而提高,那么新策略在所有状态上都将不会更差。
GridWorld:算法的可视化舞台
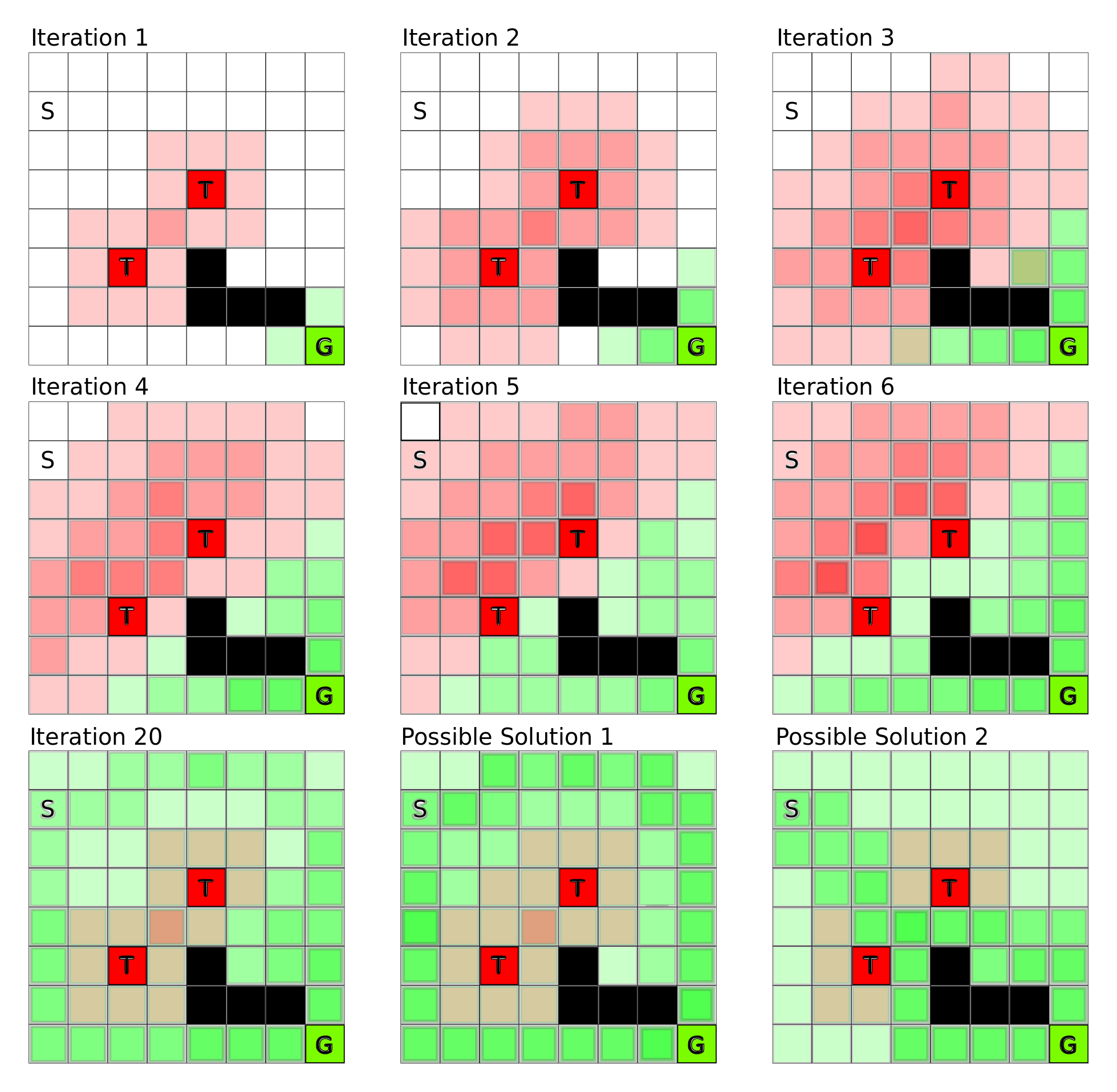
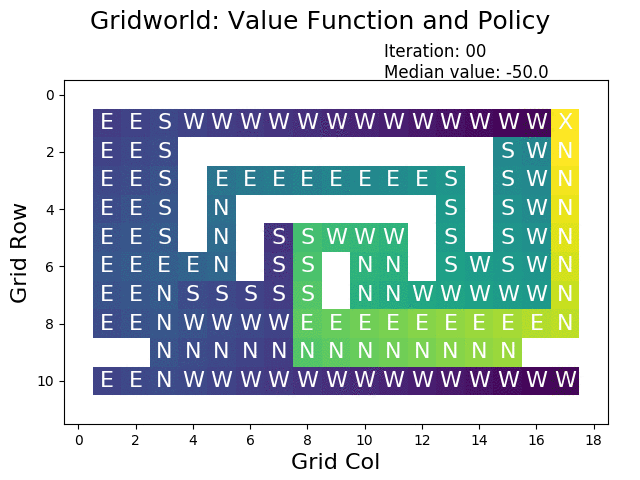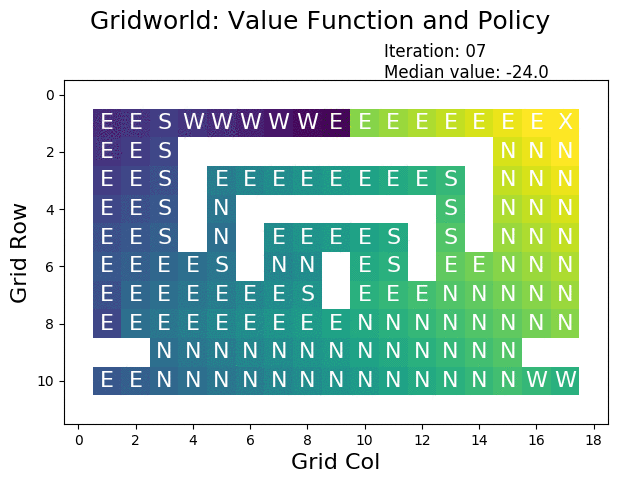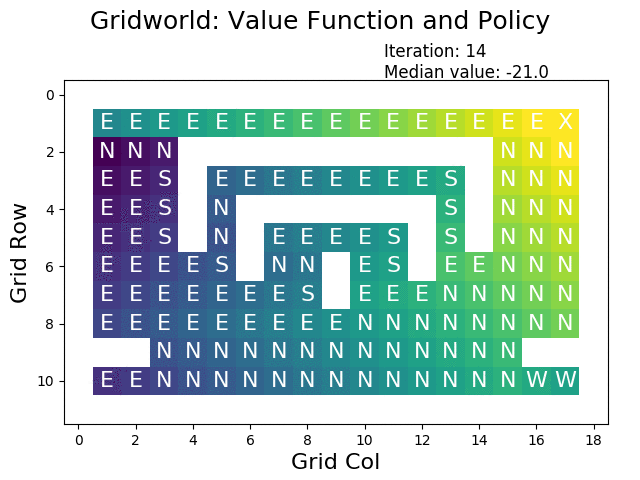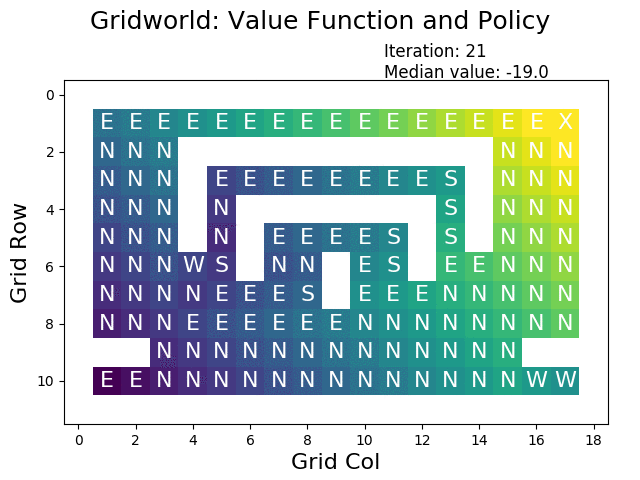
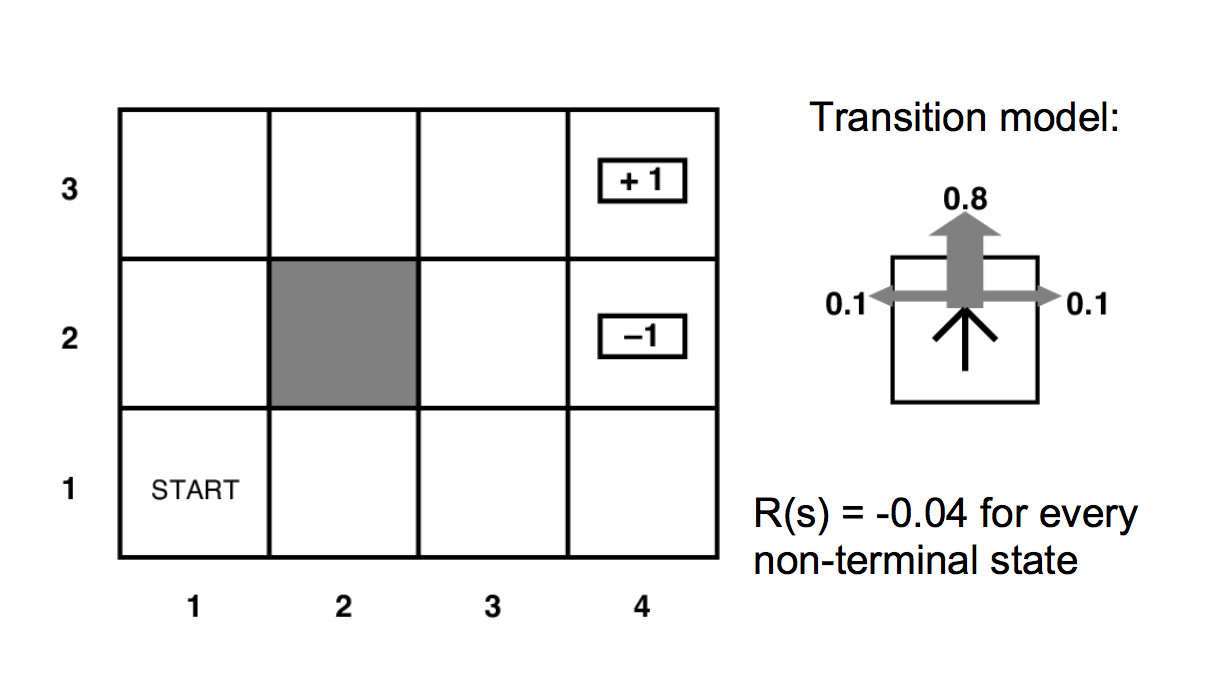
为了更直观地理解这些算法的工作原理,让我们走进GridWorld——一个简化但富有教育意义的虚拟世界。在这个4×4的网格环境中,智能体需要从起始位置导航到目标位置,同时避开障碍物和陷阱。
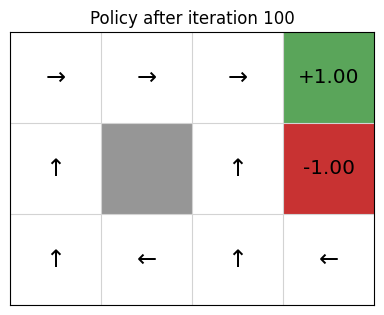
根据加州大学伯克利分校的实验,在GridWorld环境中,价值迭代算法通常在10-15次迭代内就能收敛到最优解。更有趣的是,我们可以观察到价值函数如何像波纹一样从目标状态向外扩散,逐渐为每个位置赋予合理的价值。
在典型的GridWorld设置中,目标状态被赋予+1的奖励,陷阱状态获得-1的惩罚,其他位置的奖励为-0.04(代表移动的小代价)。这种奖励设计鼓励智能体快速到达目标,同时避免不必要的绕路。
策略迭代在同样的环境中展现出不同的收敛模式。由于策略空间是离散的,策略迭代往往在更少的外层迭代中找到最优解,但每次迭代的计算成本更高。这种权衡体现了算法设计中效率与精确性之间的微妙平衡。
收敛性的数学保证
动态规划算法的收敛性不是偶然的,而是建立在坚实数学基础之上的必然结果。这个基础就是压缩映射定理(Contraction Mapping Theorem)。
根据数学分析理论,贝尔曼算子T在最大范数下是一个γ-压缩映射。这意味着对于任意两个价值函数V和U,都有:
$$||TV – TU||\infty \leq \gamma ||V – U||\infty$$
这个看似抽象的数学性质带来了两个重要的实际意义:
- 唯一性:最优价值函数是唯一的不动点
- 收敛性:从任何初始点开始,迭代过程都会收敛到这个不动点
更令人兴奋的是,我们可以精确计算收敛速度。经过k次迭代后,价值函数与最优解的误差界限为:
$$||V_k – V^||_\infty \leq \gamma^k ||V_0 – V^||_\infty$$
这个几何级数的收敛特性解释了为什么动态规划算法在实践中如此高效。以γ=0.9的常见设置为例,仅仅10次迭代就能将初始误差缩小到原来的35%,20次迭代则能缩小到12%。
维度灾难:完美理论的现实挑战
然而,如同任何强大的工具都有其适用边界,动态规划也面临着"维度灾难"这个根本性挑战。这个术语由贝尔曼本人在1961年提出,描述了高维问题中计算复杂性的指数增长现象。
最新的研究表明,当状态空间或行动空间的维度增加时,动态规划的计算需求呈指数级增长。考虑一个简单的例子:如果每个维度有10个可能的值,那么:
- 5维问题:10^5 = 100,000个状态
- 10维问题:10^10 = 100亿个状态
- 20维问题:10^20 = 1000万亿个状态
这种指数爆炸使得传统动态规划在处理现实世界的复杂问题时力不从心。一个自动驾驶汽车的状态空间可能包含位置、速度、方向、其他车辆信息等,轻易就能达到数百维的规模。

斯坦福大学的研究人员指出,现代研究正在通过多种方法应对这一挑战:
- 函数近似:使用神经网络等方法近似价值函数
- 状态聚合:将相似状态归并,减少状态空间大小
- 分层强化学习:将复杂问题分解为多个层次的子问题
- 模型压缩:保留关键特征,忽略次要细节
理论价值与实践意义
尽管面临维度灾难的挑战,动态规划在强化学习中的地位依然不可撼动。它不仅是其他算法的理论基础,更是理解强化学习本质的重要窗口。

从理论角度看,动态规划为强化学习提供了严格的数学框架。贝尔曼方程、最优性原理、收敛性定理等核心概念都源于此。正如Dimitri Bertsekas教授所言,"动态规划不仅是解决问题的方法,更是思考最优决策的方式"。
从实践角度看,虽然纯粹的动态规划难以直接应用于大规模问题,但其核心思想已经深深融入现代强化学习算法中。Q-learning、Actor-Critic、AlphaGo等算法都可以追溯到动态规划的理论根源。
现代发展与未来展望
随着计算能力的提升和算法创新的加速,动态规划正在迎来新的发展机遇。近年来出现的一些突破性进展值得关注:
近似动态规划:NASA的研究团队开发了自适应动态规划方法,成功应用于航天器控制等复杂任务。这些方法巧妙地结合了传统动态规划的理论优势和现代机器学习的计算能力。
深度强化学习融合:DeepMind的AlphaZero项目展示了如何将蒙特卡洛树搜索(一种动态规划的变种)与深度神经网络结合,在围棋、国际象棋等复杂博弈中取得突破性成果。
分布式计算优化:现代动态规划算法正在利用GPU并行计算和分布式系统,大幅提升处理能力。一些研究表明,通过智能的并行化策略,可以处理比传统方法大几个数量级的问题。

学习建议与深入方向
对于希望深入掌握动态规划的学习者,我建议遵循以下路径:
基础阶段:
- 熟练掌握马尔可夫决策过程的基本概念
- 理解贝尔曼方程的推导和直觉含义
- 手工实现简单的价值迭代和策略迭代算法
进阶阶段:
- 研究收敛性理论和误差分析
- 探索近似动态规划的各种技术
- 实验不同的函数近似方法
应用阶段:
- 将动态规划思想应用到实际问题中
- 结合深度学习技术开发新算法
- 关注最新的研究进展和应用案例

动态规划就像一首优美的数学交响曲,价值迭代、策略迭代和贝尔曼方程共同演奏着最优决策的主题。虽然维度灾难为这首乐曲增添了挑战的色彩,但正是这种挑战推动着研究者们不断创新,寻找更优雅、更高效的解决方案。
在人工智能快速发展的今天,理解动态规划不仅是掌握强化学习的必要条件,更是培养算法思维和数学直觉的重要途径。正如贝尔曼在半个多世纪前所预见的那样,最优决策的数学原理将继续指引我们探索智能系统的无限可能。