想象一下,你面前散落着一堆五颜六色的乐高积木,而你的任务是把相似的积木归类整理。这个看似简单的过程,正是机器学习中聚类算法要解决的核心问题。今天,我们就来聊聊这个神奇的数据世界,看看计算机是如何像一个细心的整理师一样,在海量数据中找到隐藏的模式和规律。
网页版:https://hqidyfzr.gensparkspace.com/
视频版:
音频版:
K-Means:最受欢迎的"群体组织者"
K-Means就像是一个经验丰富的活动组织者。你告诉它:"我要把这些参与者分成3组",它就会想方设法找到最佳的分组方案。这个过程充满了迭代的智慧。
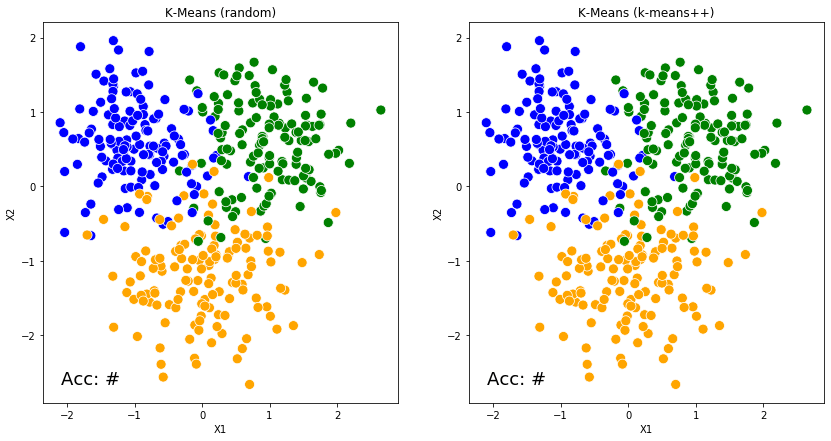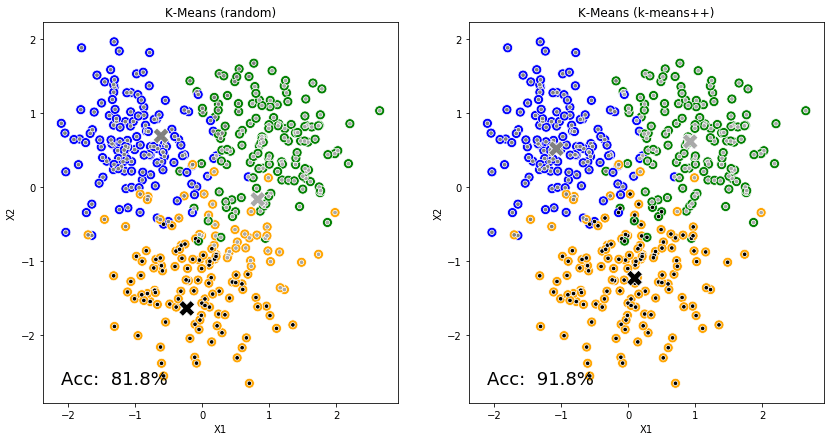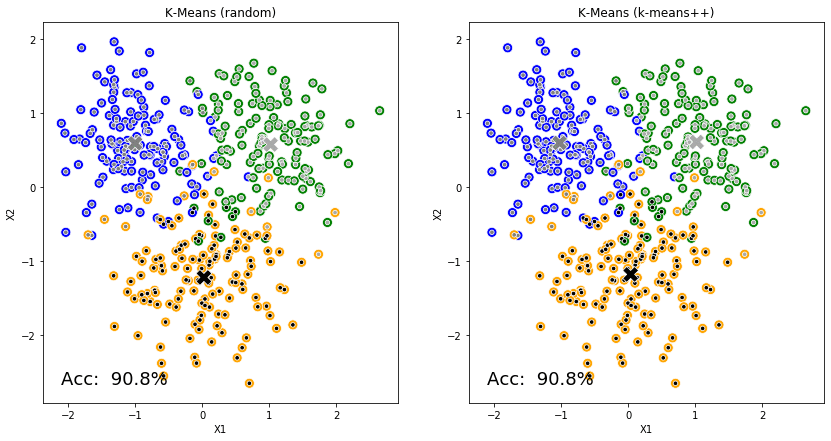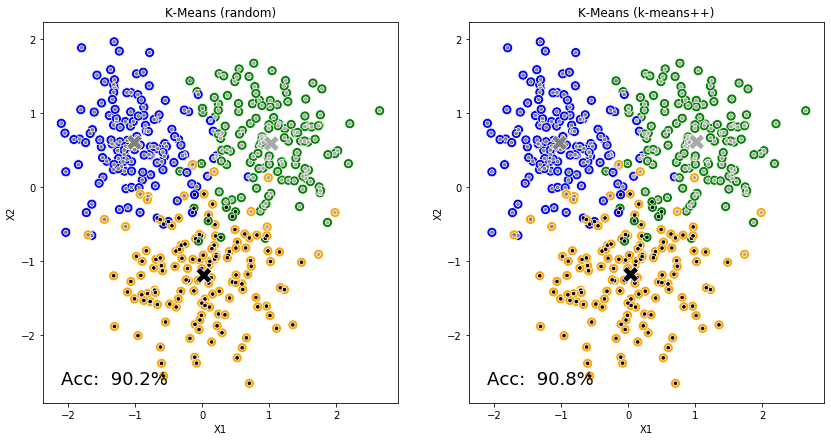
K-Means的工作原理让人想起小时候玩的"找朋友"游戏。首先,它会随机选择几个"队长"(这些就是初始的质心),然后让每个数据点找到距离自己最近的队长,加入相应的队伍。接下来最有趣的部分来了:每个队长会根据自己队伍成员的位置,调整自己的站位到队伍的中心位置。这个过程会不断重复,直到所有队长都找到了最稳定的位置。
肘部法则:寻找最佳K值的艺术
选择合适的聚类数量K,就像是为一场晚宴决定合适的餐桌数量。太少了,客人会挤得不舒服;太多了,又显得空旷浪费。肘部法则通过计算不同K值下的组内平方和(WCSS),帮助我们找到这个"恰到好处"的数字。
根据Built In的详细研究,当我们把不同K值对应的WCSS画成曲线时,通常会出现一个明显的"肘部"转折点。在这个点之前,增加聚类数量能显著降低WCSS;而过了这个点,收益就变得微乎其微了。
轮廓系数:更精确的"质量检查员"
如果说肘部法则是粗略的筛选,那么轮廓系数就是精密的质量检查。它通过计算每个数据点与同类数据的紧密程度,以及与其他类别数据的区分度,给出一个-1到1之间的分数。分数越接近1,说明聚类效果越好;接近-1则意味着数据可能被放错了位置。
层次聚类:构建数据的"家族树"
如果K-Means是快刀斩乱麻的实用主义者,那么层次聚类就是追求完美的艺术家。它不满足于简单的分组,而是要为数据构建一个完整的"家族谱系"。

层次聚类有两种策略:凝聚型(自下而上)和分裂型(自上而下)。凝聚型聚类就像是追根溯源的族谱研究,每个数据点最初都是独立的个体,然后逐渐与最相似的邻居合并,形成越来越大的家族群体。这个过程产生的树状图(dendrogram)不仅美观,更重要的是它保留了完整的聚类历史信息。
通过Scikit-learn的官方文档可以了解到,层次聚类支持多种连接策略:Ward连接最小化方差,Complete连接关注最大距离,Average连接考虑平均距离,而Single连接则着眼于最小距离。每种策略都有自己的性格特点,适用于不同形状和密度的数据集。
DBSCAN:密度的"侦探"
DBSCAN算法就像是一个经验丰富的城市规划师,它不需要你预先告诉它要建多少个社区,而是通过观察人口密度的分布,自然地识别出繁华的市中心、安静的居民区,以及偏远的郊外地带。
这个算法的核心思想令人着迷:它将数据点分为三类角色。核心点就像是社区的活跃分子,周围聚集着足够多的邻居;边界点是那些虽然自己不够活跃,但与核心点保持联系的居民;而噪声点则是那些独来独往的"隐士",它们既不是核心,也不靠近任何核心区域。
GeeksforGeeks的深入分析显示,DBSCAN只需要两个参数:ε(epsilon,邻域半径)和MinPts(最小点数)。这种简洁性使得它在处理噪声数据和发现任意形状的聚类时表现卓越,完全不同于K-Means要求的球形假设。
谱聚类:图论与线性代数的完美邂逅
谱聚类是聚类算法家族中最具数学美感的成员。它将聚类问题转化为图论问题,然后利用线性代数的工具来求解。这个过程就像是用数学的镜头重新审视数据,发现那些隐藏在高维空间中的低维结构。

谱聚类的工作流程充满了数学的诗意:首先构建数据的相似性图,然后计算图的拉普拉斯矩阵,接着求解特征值和特征向量,最后在这个新的特征空间中应用传统的聚类算法。MIT的教程详细阐述了这个过程中的数学原理,展现了理论与实践的完美结合。
聚类评估:如何判断算法的"成绩单"
即使是最好的聚类算法,也需要有评估标准来衡量其表现。这就像是给学生的作业打分,我们需要客观的评价指标。
轮廓系数:个体与群体的和谐度
轮廓系数通过比较每个数据点与同类数据的相似性以及与其他类别数据的差异性,给出一个综合评分。计算公式为:S = (b-a) / max(a,b),其中a是点与同类其他点的平均距离,b是点与最近邻类的平均距离。
Calinski-Harabasz指数:类间与类内方差的平衡艺术
Wikipedia的详细介绍显示,这个指数通过计算类间方差与类内方差的比值来评估聚类质量。较高的CH指数表明聚类间差异明显,聚类内紧密度高,这正是我们希望看到的理想状态。
实战应用:从理论到实践的桥梁
现在,让我们用Python和Scikit-learn将这些算法付诸实践。以经典的鸢尾花数据集为例:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.cluster import KMeans, AgglomerativeClustering, DBSCAN, SpectralClustering
from sklearn.metrics import silhouette_score, calinski_harabasz_score
# 加载数据
iris = datasets.load_iris()
X = iris.data
# K-Means聚类
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans_labels = kmeans.fit_predict(X)
# 层次聚类
hierarchical = AgglomerativeClustering(n_clusters=3)
hierarchical_labels = hierarchical.fit_predict(X)
# DBSCAN聚类
dbscan = DBSCAN(eps=0.5, min_samples=5)
dbscan_labels = dbscan.fit_predict(X)
# 谱聚类
spectral = SpectralClustering(n_clusters=3, random_state=42)
spectral_labels = spectral.fit_predict(X)
# 评估结果
algorithms = ['K-Means', 'Hierarchical', 'DBSCAN', 'Spectral']
labels_list = [kmeans_labels, hierarchical_labels, dbscan_labels, spectral_labels]
for alg, labels in zip(algorithms, labels_list):
if len(set(labels)) > 1: # 确保有多个聚类
silhouette_avg = silhouette_score(X, labels)
calinski_avg = calinski_harabasz_score(X, labels)
print(f"{alg}: 轮廓系数={silhouette_avg:.3f}, CH指数={calinski_avg:.3f}")
这段代码展示了如何在同一数据集上比较不同算法的表现,通过定量指标来评估各自的优劣。
算法选择的智慧:没有银弹,只有合适的工具
选择聚类算法就像是为不同的任务选择合适的工具。K-Means适合处理球形分布的大型数据集,执行效率高;层次聚类在小型数据集上表现出色,能提供丰富的结构信息;DBSCAN擅长处理噪声数据和发现任意形状的聚类;而谱聚类则在处理复杂的非线性结构时展现出独特优势。
Scikit-learn的聚类算法比较通过可视化展示了各种算法在不同数据模式下的表现,这为我们的选择提供了直观的参考。
未来展望:聚类算法的新地平线
随着大数据时代的到来,聚类算法也在不断进化。深度聚类将神经网络与传统聚类相结合,能够处理更复杂的高维数据;增量聚类算法可以处理流式数据,适应数据的动态变化;而多视图聚类则能够整合来自不同源的信息,提供更全面的数据理解。
聚类算法的魅力在于它能够在没有标签的数据中发现隐藏的模式,就像是数据科学家的"第三只眼",帮助我们看到数据背后的本质结构。无论是市场细分、社交网络分析,还是基因序列研究,聚类算法都在默默地发挥着重要作用。
掌握这些算法不仅是技术技能的提升,更是培养数据思维的重要途径。当我们学会用聚类的眼光看待世界时,就会发现原来复杂的现象背后,往往隐藏着简洁而美妙的数学规律。
