一个颠覆传统信息论的新视角
最近,我读到一篇让我兴奋得睡不着觉的论文。

它来自卡内基梅隆大学和纽约大学的联合团队,标题叫《From Entropy to Epiplexity》。这篇论文试图回答一个看似简单、实则困扰整个AI行业的问题:
数据到底"值钱"在哪里?
你可能会说,这还用问吗?数据量越大越好,信息量越多越好。但如果真是这样,为什么有些数据训练出来的模型聪明得像天才,有些数据训练出来的模型蠢得像榆木疙瘩?
让我从一个真实的困惑讲起。
第一章:三个让人抓狂的怪现象
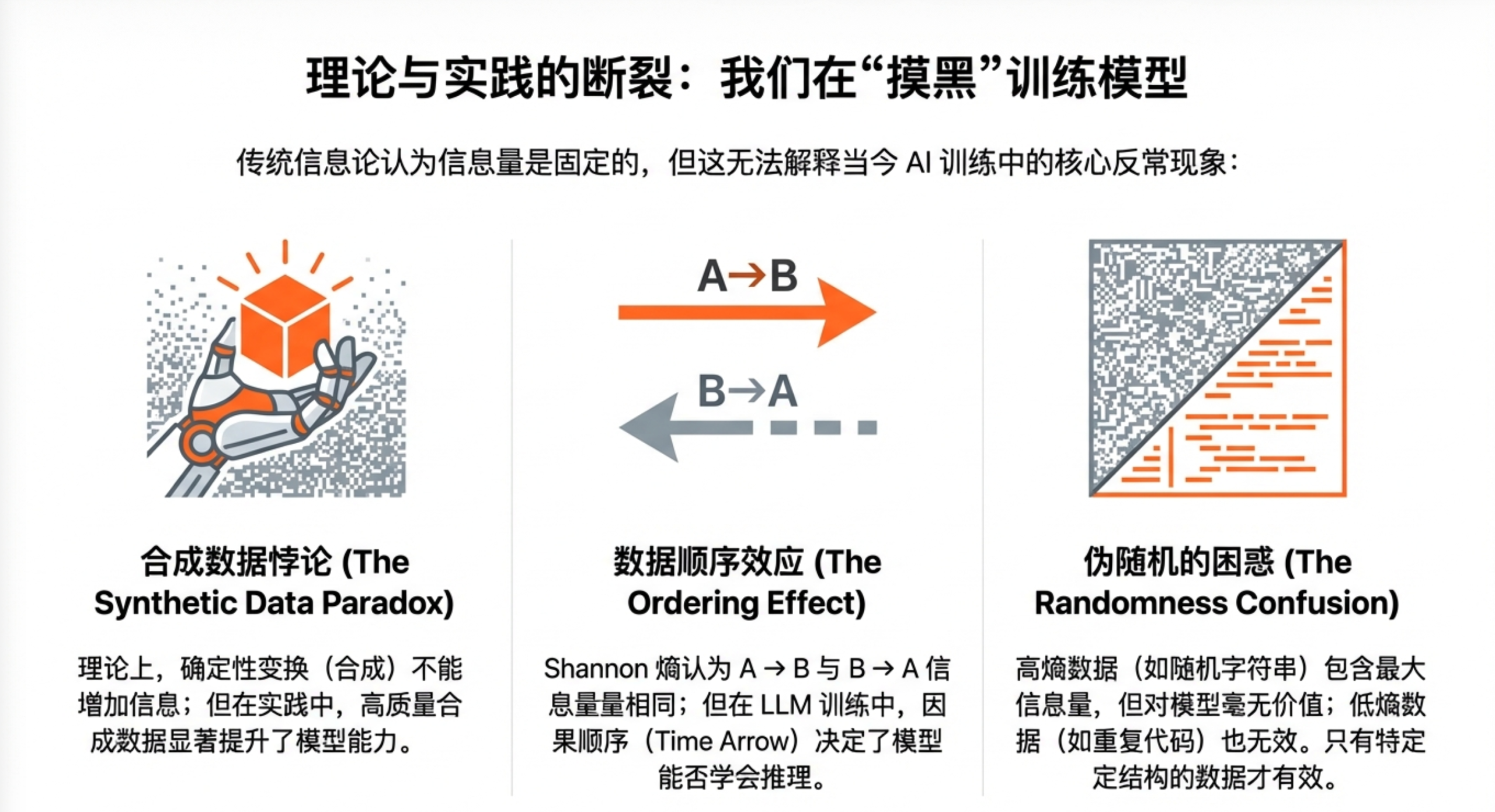
怪现象一:合成数据凭什么比真数据还好用?
AlphaZero是围棋史上最强的AI。但它学习围棋的方式很奇怪——它从来没看过一盘人类棋谱,只是对着规则自己跟自己下棋。
按照传统信息论的说法,围棋规则就那么几条,信息量微乎其微。自我对弈只是确定性的计算过程,不会"凭空产生"新信息。那AlphaZero脑子里那些精妙绝伦的棋艺是从哪来的?
同样的问题也出现在大模型训练中。真实世界的高质量数据越来越稀缺,大家开始用合成数据。奇怪的是,有时候合成数据训练出来的模型比用原始数据还强。但合成数据不就是原始数据的"加工品"吗?加工怎么能增加信息?
怪现象二:同样的内容,换个顺序就学不会了?
把一篇英文文章正着读和倒着读,信息量应该一样吧?毕竟字母都没变,只是顺序反了。

但大语言模型不这么看。让GPT从左到右预测下一个词,它学得飞快;让它从右到左预测前一个词,效果断崖式下跌。同样的数据,同样的模型,只是方向变了,学习效果就天差地别。
密码学家早就知道这个秘密:有些函数"正向"算很容易,"逆向"算几乎不可能。但传统信息论说,双向的信息量应该是对称的啊?
怪现象三:模型学到的东西,比数据里有的还多?
Conway的生命游戏,规则简单到只有一句话:一个细胞如果有2-3个邻居就存活,否则死亡。

但当你运行这个规则,神奇的事情发生了——屏幕上出现了"滑翔机"、“脉冲星”、“飞船"等各种复杂结构,它们有自己的"物种分类"和"行为模式”。如果你训练一个神经网络来预测生命游戏的下一帧,它会学到这些"物种"的概念,尽管规则里根本没提过什么滑翔机。
模型学到的东西,比生成数据的规则复杂得多。这怎么可能?
第二章:传统信息论的"原罪"
这三个怪现象有一个共同的根源:传统信息论假设观察者拥有无限的计算能力。
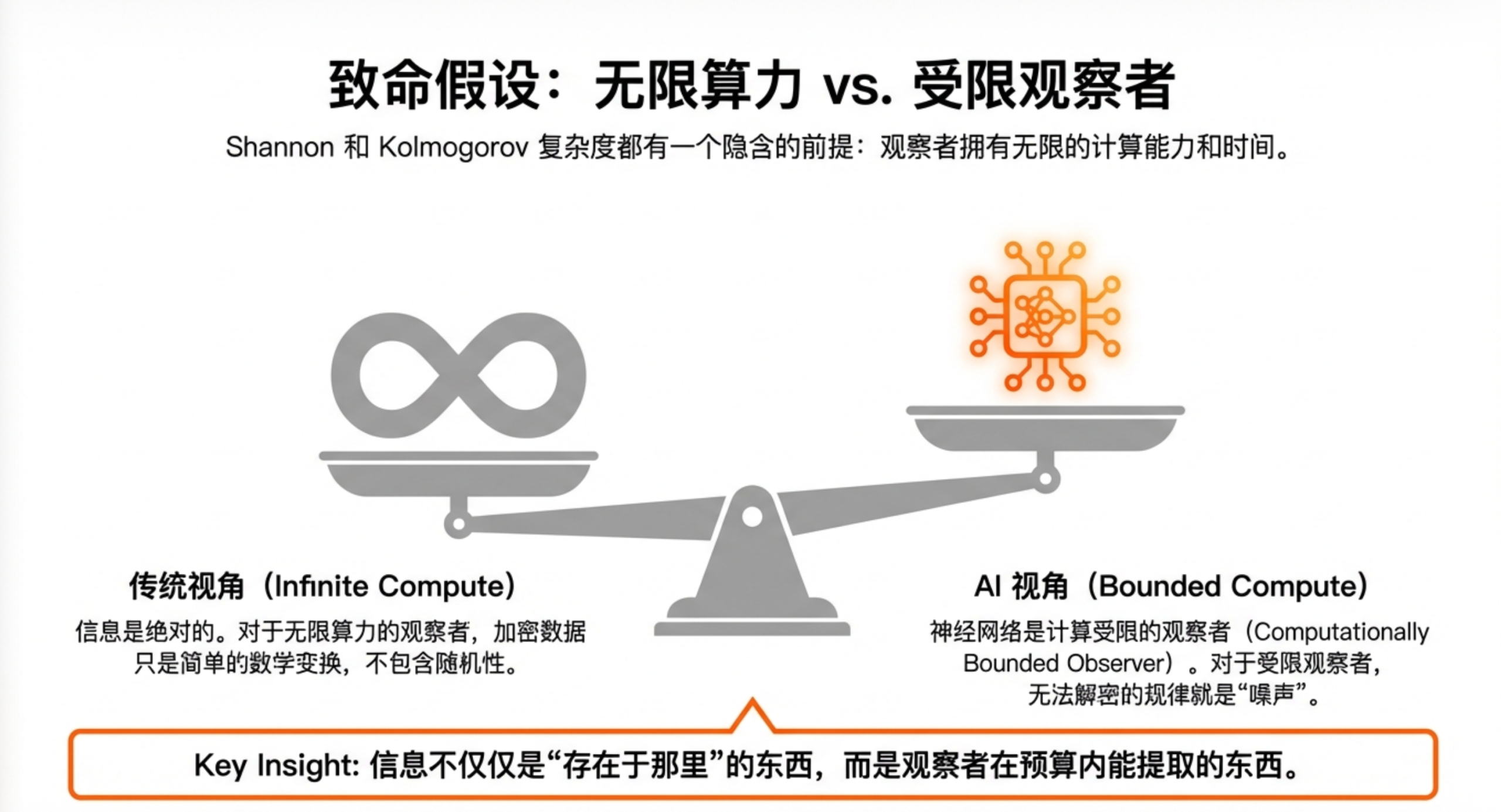
Shannon在1948年创立信息论时,关心的是"通信"问题——如何用最少的比特把消息从A传到B。他不关心接收方是人还是机器,更不关心接收方的计算能力。
Kolmogorov复杂度走得更远,它把信息定义为"能生成这个对象的最短程序"。听起来很优雅,但有个致命问题:找到那个最短程序可能需要无穷的计算时间。
在这两个框架里,一个密码学安全的伪随机数序列(比如你电脑上的随机数生成器输出)的"真正信息量"很小——因为它可以用一个短程序加一个种子生成。但对于任何实际的观察者来说,这串数字和真正的随机数没有任何区别,你根本学不到任何规律。
这就是问题所在:传统信息论度量的是"上帝视角"的信息,而不是"凡人视角"的信息。
第三章:把计算能力纳入信息的定义
论文的核心洞见是:信息必须相对于观察者的计算能力来定义。
想象你是一个只有多项式时间计算能力的观察者(这基本上就是所有现实中的计算机和神经网络)。面对一份数据,你能从中提取的信息分为两部分:
第一部分:你怎么也学不会的随机噪声
不管你多努力,不管你的模型多大,有些东西就是预测不了。比如API密钥、哈希值、加密后的数据——它们对你来说就是纯粹的"熵",毫无规律可言。
论文把这部分叫做时间受限熵(Time-Bounded Entropy),记作H_T。
第二部分:你能学进脑子里的结构
有些数据虽然也有噪声,但里面藏着可以被发现、被复用的规律。比如自然语言中的语法结构、代码中的编程范式、棋谱中的战术套路。这些东西可以被"压缩"进你的模型参数里,成为可迁移的知识。
论文把这部分叫做Epiplexity(认知复杂度),记作S_T。
两个名字都有点拗口,但概念其实很直观:
- H_T = 学不会的(对你来说的真随机)
- S_T = 学得会的(对你来说的真结构)
最妙的是,这个划分依赖于观察者是谁。同一份数据,对算力强的观察者可能结构更多、噪声更少;对算力弱的观察者可能正好相反。
第四章:三个怪现象终于有了解释
有了这套新框架,前面的三个怪现象突然变得清晰了。
解释一:计算可以"制造"结构信息
AlphaZero的自我对弈确实是确定性计算,但这个计算过程会产生大量的棋局状态——对于一个计算受限的观察者来说,这些状态里蕴含的战术结构是全新的、可学习的。
换句话说,计算过程把"隐藏在规则里的结构"显式地展开了出来。规则本身可能很简单,但规则运行产生的数据却可以有极高的epiplexity。
合成数据同理。好的合成数据不是简单地复制原始数据,而是通过计算过程把原始数据中隐含的结构"放大"或"显化",让模型更容易学到。
解释二:顺序决定了什么是可学的
传统信息论说I(X;Y) = I(Y;X),先看X再看Y和先看Y再看X的信息量一样。
但在计算受限的世界里,这个等式不成立。
从左到右读英文时,每个词都在"预测"下一个词——主语预测动词,动词预测宾语,这是符合人类语言生成逻辑的。模型沿着这个方向学,自然事半功倍。
从右到左读时,模型要从结果"反推"原因,这就像让你从加密结果反推明文——理论上信息都在那里,但实际上你根本学不会。
数据的呈现顺序,本身就是一种"结构注入"。好的顺序能让结构更容易被计算受限的观察者发现。
解释三:学习本身就是结构发现
当神经网络预测生命游戏的下一帧时,它不会傻傻地记住每个像素的变化规律。那样太低效了。
为了压缩数据、提高预测准确率,网络会自发地"发明"一些中间概念——比如"这是一个滑翔机,它会向右下角移动"。这些概念比底层规则更抽象、更有用,也更容易迁移到其他任务。
这就是为什么模型可以学到比生成规则更多的东西:它不是在复刻规则,而是在发现规则运行时涌现的结构。
第五章:怎么测量数据的"真正价值"?
理论再漂亮,不能落地也是空谈。论文最实用的部分是给出了两种测量epiplexity的方法。
方法一:看训练曲线的"面积"
这是一个简单粗暴但很有效的启发式方法。

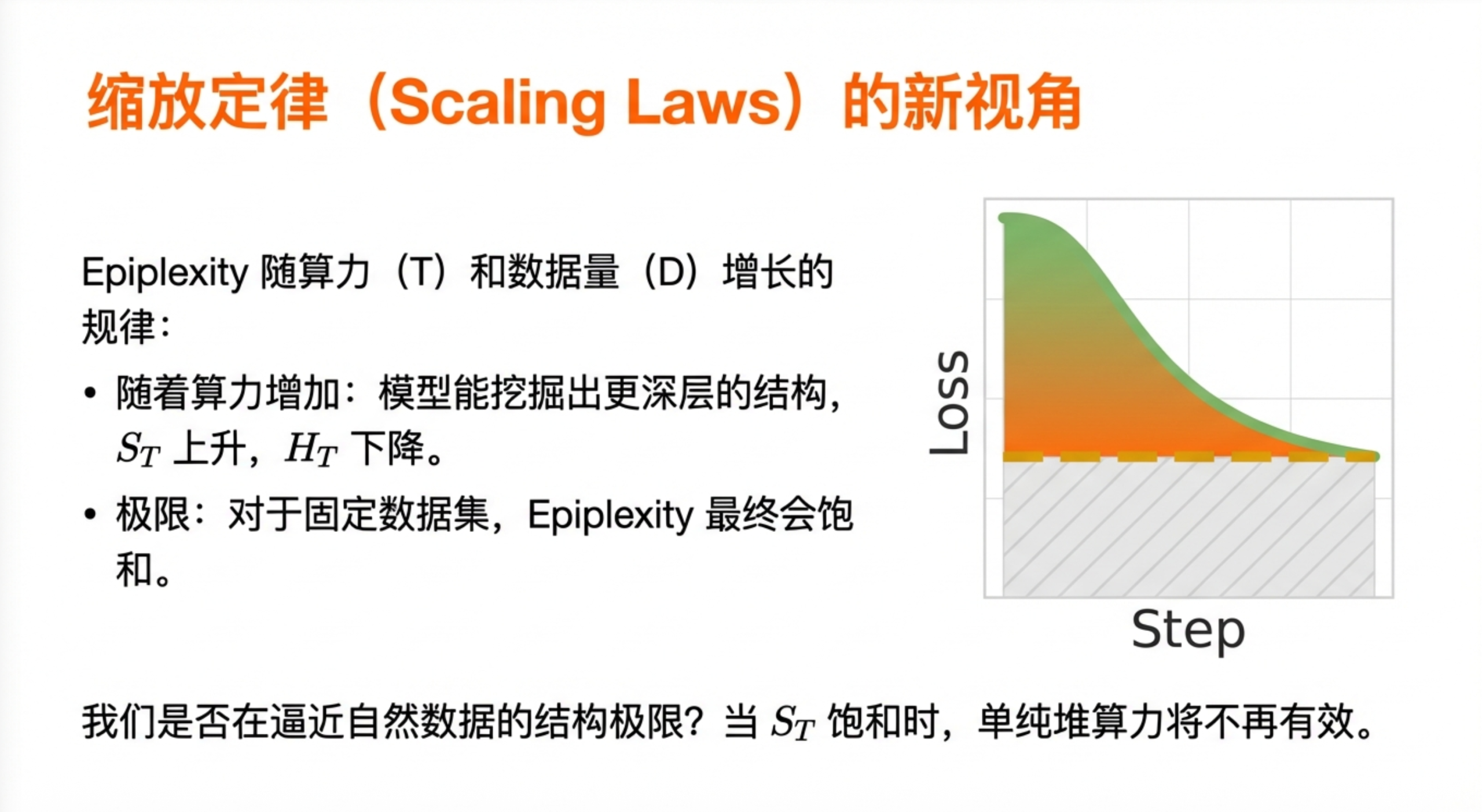
当你训练一个模型时,loss曲线通常是先高后低。刚开始模型什么都不懂,loss很高;训练到最后,模型学会了数据中的规律,loss降到最低。
论文的洞见是:loss曲线下降的过程,就是模型在"吸收"结构信息的过程。
具体来说,把loss曲线和最终loss之间的面积算出来,这个面积就近似等于模型从数据中学到的结构信息量。
Loss
↑
│╲
│ ╲
│ ╲___________ ← 最终loss
│ ████████ ← 这块面积 ≈ 学到的结构
│
└─────────────→ 训练步数
这个方法的好处是计算代价低,只要你有训练日志就能算。缺点是比较粗糙,只能做相对比较,不能给出精确值。
方法二:教师-学生的KL散度累积
这是一个更严谨的方法,但计算代价也更高。
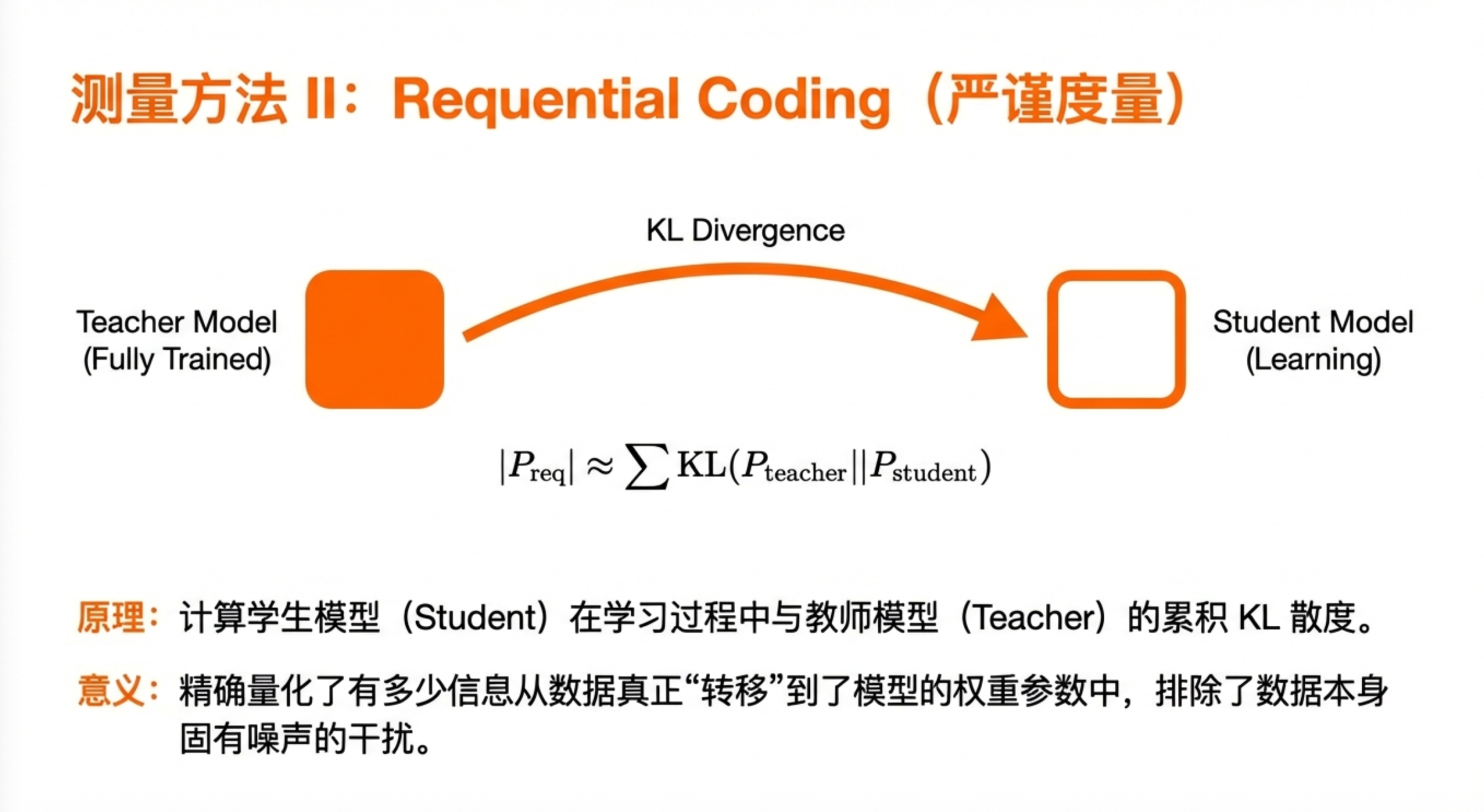
想象有两个模型:一个是"教师",已经看过全部数据;一个是"学生",正在一点一点学习数据。在每个时间点,我们比较教师和学生对数据的预测分布,计算它们之间的KL散度。
把整个训练过程中的KL散度累积起来,就得到了学生从数据中"学到"的结构信息的严格上界。
这个方法有理论保障,但需要额外训练一个教师模型,计算成本翻倍。
第六章:这对我们意味着什么?
如果你是AI从业者,这篇论文给你三个重要启示:
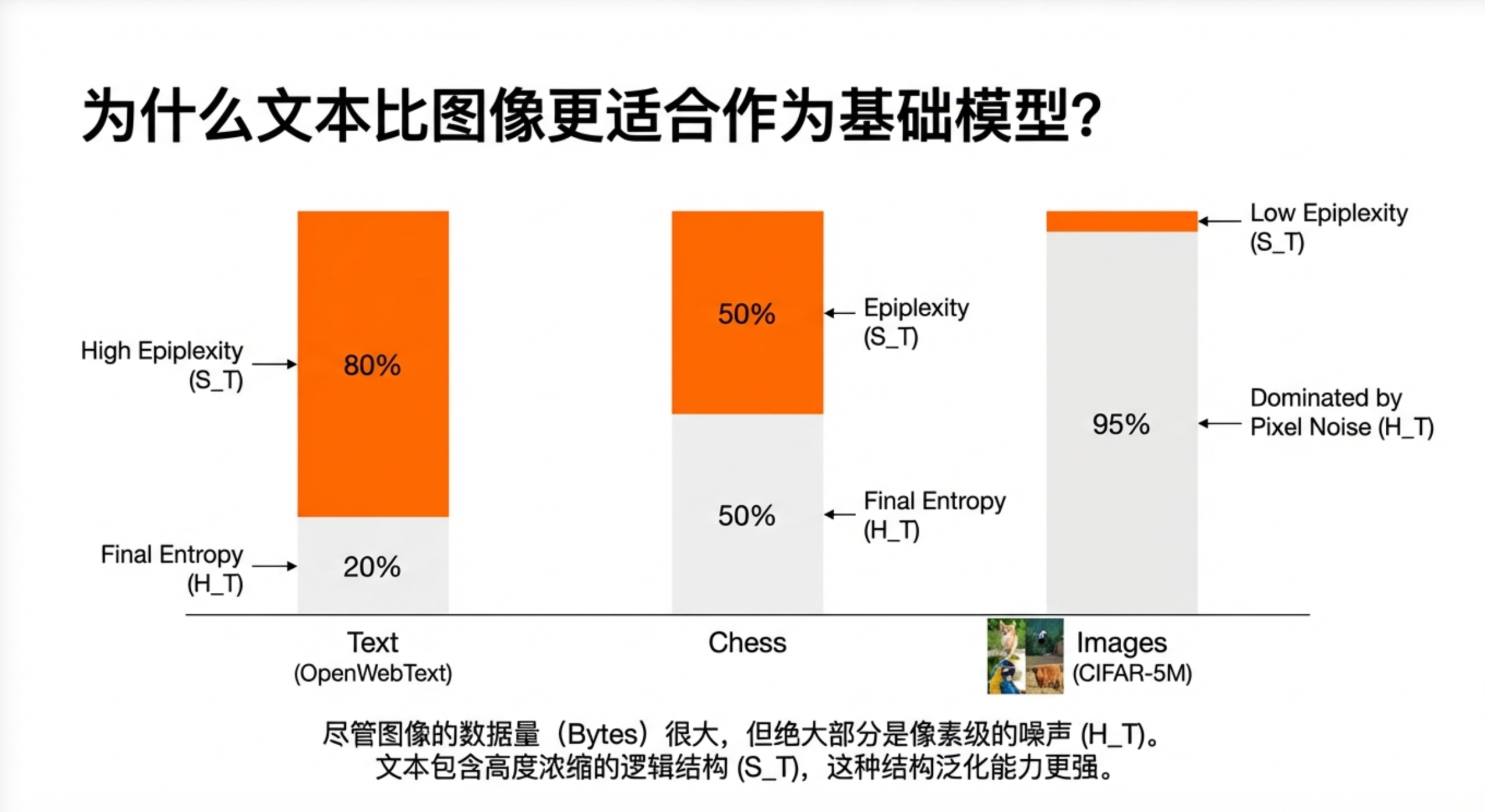
启示一:数据选择比你想象的更重要
传统观点认为模型架构和训练算法是核心,数据只要"量大管饱"就行。但论文告诉我们,数据的选择可能比模型的选择更关键。
高epiplexity的数据(结构丰富、可学习的规律多)训练出的模型,在分布外任务上表现更好。这不是因为数据量大,而是因为模型从中学到了更多可复用的"电路"和"子程序"。
实操建议:在筛选训练数据时,不要只看数据量和多样性,还要考虑数据是否能诱导模型学到可迁移的结构。可以用loss曲线面积法快速估计不同数据源的epiplexity。
启示二:数据的表示和顺序是可优化的杠杆
同一份数据,换一种表示方式或呈现顺序,学习效果可能截然不同。
论文在国际象棋数据上做了实验:同样的棋谱,用不同的符号表示、不同的排列顺序,模型学到的结构量差异显著——而且高epiplexity的表示方式确实带来了更好的分布外泛化。
实操建议:不要把数据格式当作固定不变的东西。尝试不同的tokenization方式、不同的排列顺序,用epiplexity作为指标来选择最优的数据表示。
启示三:合成数据的价值在于"结构显化"
合成数据不是用来增加数据量的,而是用来增加可学结构的。
好的合成数据应该把原始数据中隐含的、难以直接学习的结构"翻译"成更容易被模型捕捉的形式。如果合成数据只是原始数据的简单变换,没有显化新的结构,那它的价值就很有限。
实操建议:评估合成数据时,不要只看它是否"像"真实数据,而要看它是否能让模型学到新的、可复用的结构。可以对比原始数据和合成数据的epiplexity差异。
尾声:从"数据越多越好"到"结构越可学越好"
回顾整篇论文,它最大的贡献是提供了一个新的思考框架:
数据的价值不在于它包含多少"信息",而在于它能让特定的观察者学到多少"结构"。

这是一个观察者依赖的、计算感知的信息论。它承认现实世界的计算资源是有限的,也承认同一份数据对不同能力的观察者价值不同。
对于AI从业者来说,这意味着一个范式转变:
不要问"这份数据熵有多高",而要问"这份数据能不能让我的模型长出可复用的结构"。
这个问题的答案,决定了你的模型能走多远。