我至今记得那个春天的午后,当我第一次真正理解了矩阵变换的几何意义时,那种认知的震撼让我久久不能平静。突然间,那些干巴巴的符号和公式,在我脑海中变成了具象的空间拉伸和旋转,仿佛宇宙的秘密在那一刻向我敞开。今天,我想邀请你和我一起,踏上这段穿越线性代数核心的奇妙旅程,从向量空间的基础概念出发,一路前行到大模型中复杂的矩阵计算。
网页版:https://abyvravb.gensparkspace.com
视频版:https://www.youtube.com/watch?v=erIgwxjFWGY
音频版:https://notebooklm.google.com/notebook/c0447e34-4222-4aee-b2c7-9d3982ff26da/audio
向量空间:万物的源头
向量空间是线性代数的基石,它不仅仅是一些箭头的集合,而是满足特定运算规则的数学结构。想象一下,当你站在一个空旷的平原上,可以向任何方向行走任意距离,这个平原就像一个向量空间,你的每一步都是一个向量操作。
向量空间必须满足八条公理,包括加法封闭性、标量乘法封闭性、加法结合律等。这些看似繁琐的规则其实定义了一个优雅的数学世界,让我们能够以一致的方式处理各种数学对象。
在实际应用中,最常见的向量空间是 R^n,也就是 n 维实数空间。比如 R^2 是我们熟悉的平面,R^3 是我们生活的三维空间。但向量空间的魅力在于它的抽象性——函数、多项式、矩阵都可以构成向量空间,这种统一性让数学分析变得异常优美。
"向量空间是一个集合,其中的元素可以相加并可以被标量所乘,且满足一系列公理性质。这些性质确保了向量空间中的运算表现得像我们熟悉的欧几里得空间中的向量那样。" Khan Academy
矩阵运算:变换的语言
如果说向量空间是舞台,那么矩阵就是这个舞台上的魔术师,能够将整个空间进行变换。我常常将矩阵想象成一台神奇的机器,它接收一个向量作为输入,然后输出另一个向量。
矩阵乘法
矩阵乘法是最基本也是最强大的矩阵运算。当矩阵 A 乘以向量 v 时,实际上是将向量 v 在由矩阵 A 定义的新坐标系中表示出来。这听起来很抽象,但几何上非常直观:矩阵 A 的每一列就是原始基向量在新坐标系中的位置。
以两个矩阵相乘为例:$C = AB$,其中 $C_{ij} = \sum_k A_{ik}B_{kj}$。表面上看,这只是一系列乘法和加法,但实际上,这代表了两个线性变换的复合——先应用变换 B,再应用变换 A。
import numpy as np
# 定义两个矩阵
A = np.array([[2, 1],
[1, 3]])
B = np.array([[1, 0],
[0, 2]])
# 矩阵乘法
C = np.dot(A, B)
print("矩阵乘法结果:\n", C)
# 验证变换的复合效果
v = np.array([1, 1])
result1 = np.dot(A, np.dot(B, v))
result2 = np.dot(C, v)
print("先B后A的变换结果:", result1)
print("复合变换C的结果:", result2)
矩阵求逆
矩阵求逆可以看作是"撤销"一个变换。如果矩阵 A 将空间变换成新的形状,那么它的逆矩阵 A^(-1) 就会将空间变回原来的样子。数学上,如果 $AA^{-1} = A^{-1}A = I$(单位矩阵),则 A^(-1) 是 A 的逆。
不是所有矩阵都有逆,只有行列式不为零的方阵(可逆矩阵)才有逆矩阵。这告诉我们一个深刻的道理:只有那些不会"压缩"空间维度的变换才能被完全撤销。
# 计算矩阵的逆
A_inv = np.linalg.inv(A)
print("A的逆矩阵:\n", A_inv)
# 验证AA^(-1) = I
I = np.dot(A, A_inv)
print("A乘以A的逆:\n", np.round(I, decimals=10)) # 使用round处理浮点误差
矩阵分解
矩阵分解就像是将一个复杂的变换拆解成几个简单的步骤。常见的分解方法包括LU分解、QR分解、特征值分解和奇异值分解(SVD)。
LU分解将矩阵分解为一个下三角矩阵(L)和一个上三角矩阵(U)的乘积,这对求解线性方程组特别有效。QR分解将矩阵分解为一个正交矩阵(Q)和一个上三角矩阵(R)的乘积,常用于最小二乘问题。
# LU分解
from scipy.linalg import lu
P, L, U = lu(A)
print("LU分解结果:")
print("L =\n", L)
print("U =\n", U)
print("验证 P.L.U =? A\n", np.dot(P, np.dot(L, U)))
特征值分解:矩阵的DNA
特征值和特征向量是理解矩阵深层本质的关键。当矩阵 A 作用在它的特征向量 v 上时,只会改变这个向量的长度,而不改变它的方向:$Av = \lambda v$,其中 $\lambda$ 是特征值。
这就像是发现了矩阵的"主轴"——沿着这些特殊方向,矩阵的作用简单地表现为伸缩。特征值分解可以将一个n×n的方阵A表示为:$A = PDP^{-1}$,其中D是对角矩阵,对角线上的元素即为特征值,P的列是对应的特征向量。
# 特征值分解
eigenvalues, eigenvectors = np.linalg.eig(A)
print("特征值:", eigenvalues)
print("特征向量:\n", eigenvectors)
# 验证 Av = λv
for i in range(len(eigenvalues)):
v = eigenvectors[:, i]
Av = np.dot(A, v)
lambda_v = eigenvalues[i] * v
print(f"验证特征向量 {i+1}:")
print("Av =", Av)
print("λv =", lambda_v)
print("是否相等:", np.allclose(Av, lambda_v))
特征值分解在多个领域都有重要应用,如主成分分析(PCA)、振动分析、量子力学等。它让我们能够把复杂的矩阵变换简化为一系列简单的伸缩和旋转操作。
SVD在AI中的应用:降维之美
奇异值分解(SVD)是线性代数中最强大的工具之一,尤其在机器学习和数据科学中。它可以将任何矩阵分解为三个矩阵的乘积:$A = U\Sigma V^T$,其中U和V是正交矩阵,Σ是对角矩阵,对角线上的元素称为奇异值。
SVD的几何意义非常优雅:它将一个线性变换分解为旋转(由V^T完成)、拉伸(由Σ完成)和另一个旋转(由U完成)。
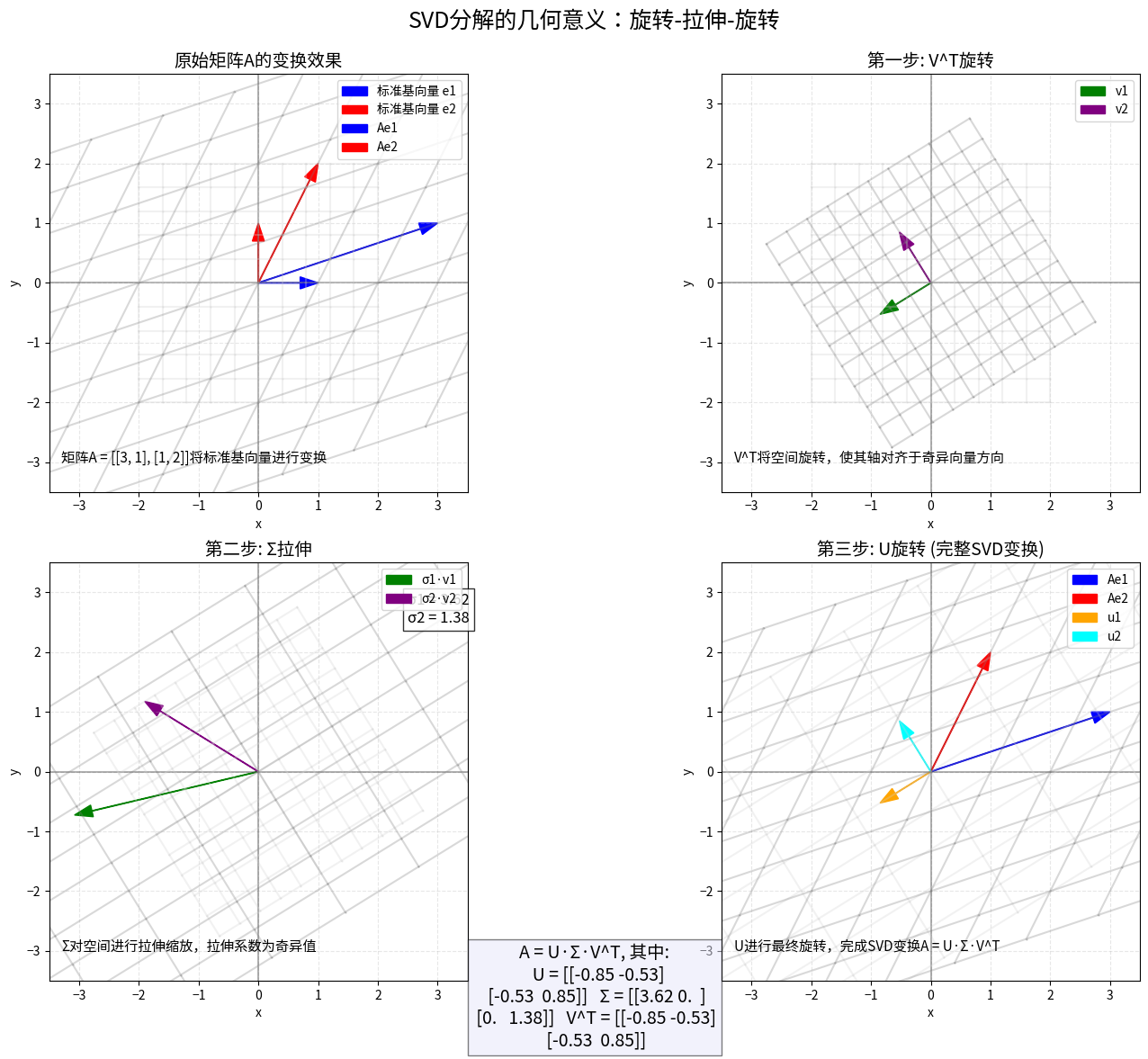
在AI领域,SVD是主成分分析(PCA)的核心。PCA通过找到数据方差最大的方向,实现降维的同时保留最多信息。具体来说,我们可以只保留最大的几个奇异值对应的成分,从而得到原始数据的低维表示。
# 使用SVD进行PCA降维
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
# 加载鸢尾花数据集并标准化
iris = load_iris()
X = iris.data
X_std = StandardScaler().fit_transform(X)
# 执行SVD
U, s, Vt = np.linalg.svd(X_std, full_matrices=False)
# 选择前两个主成分
X_pca = np.dot(X_std, Vt.T[:, :2])
# 查看奇异值(方差解释比例)
explained_variance = s**2 / np.sum(s**2)
print("各主成分解释的方差比例:", explained_variance)
print("前两个主成分解释的总方差比例:", np.sum(explained_variance[:2]))
在图像压缩中,SVD同样大显神威。我们可以用较少的奇异值来近似表示一个图像,从而实现压缩。奇异值越大,对应的信息越重要,保留的奇异值个数决定了压缩后的质量和大小。大数据时代,降维不仅是压缩数据的手段,更是揭示数据潜在结构的窗口。
大模型中的注意力机制:矩阵计算的华丽舞台
如果说传统机器学习是矩阵计算的初级应用,那么现代大型语言模型中的注意力机制则是矩阵计算的终极表演。注意力机制允许模型在处理序列数据时,关注最相关的部分,这一切都通过一系列精妙的矩阵运算来实现。
在Transformer架构中,注意力机制首先将输入转换为三个矩阵:查询(Query)、键(Key)和值(Value),分别用Q、K、V表示。然后通过计算Q和K的相似度,得到注意力权重,最后用这些权重对V进行加权求和。
具体计算过程如下:
- 注意力分数 = $QK^T / \sqrt{d_k}$,其中$d_k$是键向量的维度
- 应用softmax函数,将分数转换为权重
- 最终输出 = softmax(注意力分数) × V
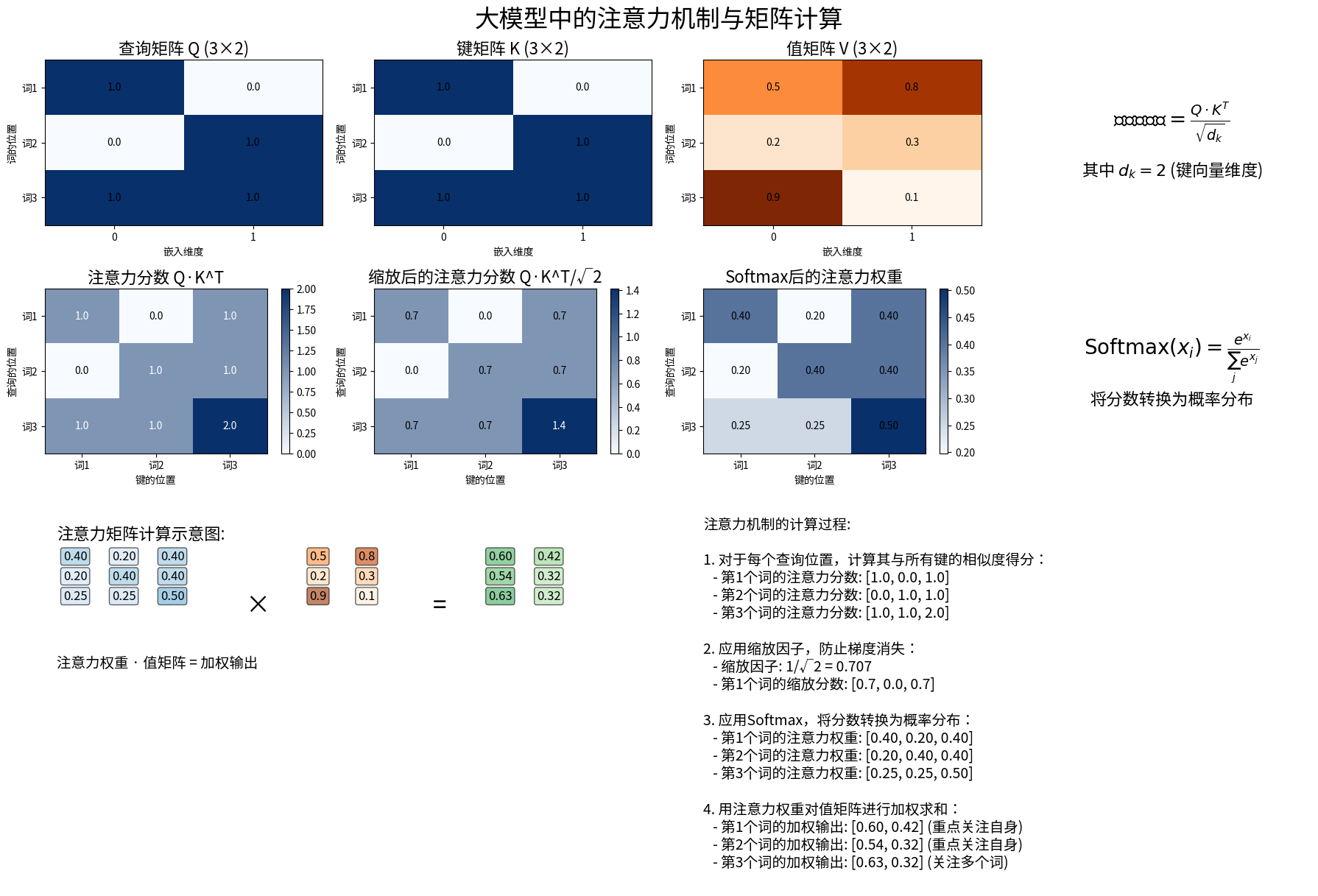
这种机制实现了一种"动态加权",使模型能够根据上下文自动决定应该关注的信息。例如,在处理"银行"这个词时,根据前后文的不同,模型会自动判断它是指"金融机构"还是"河岸"。
# 简化版的自注意力机制实现
def self_attention(X, mask=None):
# X shape: (batch_size, seq_length, d_model)
# 线性投影得到Q, K, V
Q = np.dot(X, Wq) # Wq是学习的权重矩阵
K = np.dot(X, Wk)
V = np.dot(X, Wv)
# 计算注意力分数
d_k = K.shape[-1]
scores = np.matmul(Q, K.transpose(0, 2, 1)) / np.sqrt(d_k)
# 应用mask(如果有)
if mask is not None:
scores = scores + (mask * -1e9)
# 应用softmax
weights = softmax(scores, axis=-1)
# 加权求和
output = np.matmul(weights, V)
return output, weights
在大模型训练过程中,这些矩阵运算被成千上万次地执行,每一次都在帮助模型理解和生成更复杂的语言模式。得益于现代GPU的并行计算能力和优化的矩阵库,这些计算能够高效地完成。
注意力机制的强大之处在于,它不仅能处理局部关系,还能捕获序列中任意两个位置之间的依赖关系,这是传统RNN和CNN模型难以做到的。这也是为什么Transformer模型在机器翻译、文本生成等任务上表现卓越的原因。
图像变换的数学模型:矩阵在计算机视觉中的应用
在计算机视觉中,图像变换如旋转、缩放和平移是基础操作,这些操作都可以用矩阵来表示。当我们处理数字图像时,图像实际上是一个像素值矩阵,而变换就是对这个矩阵进行特定的操作。
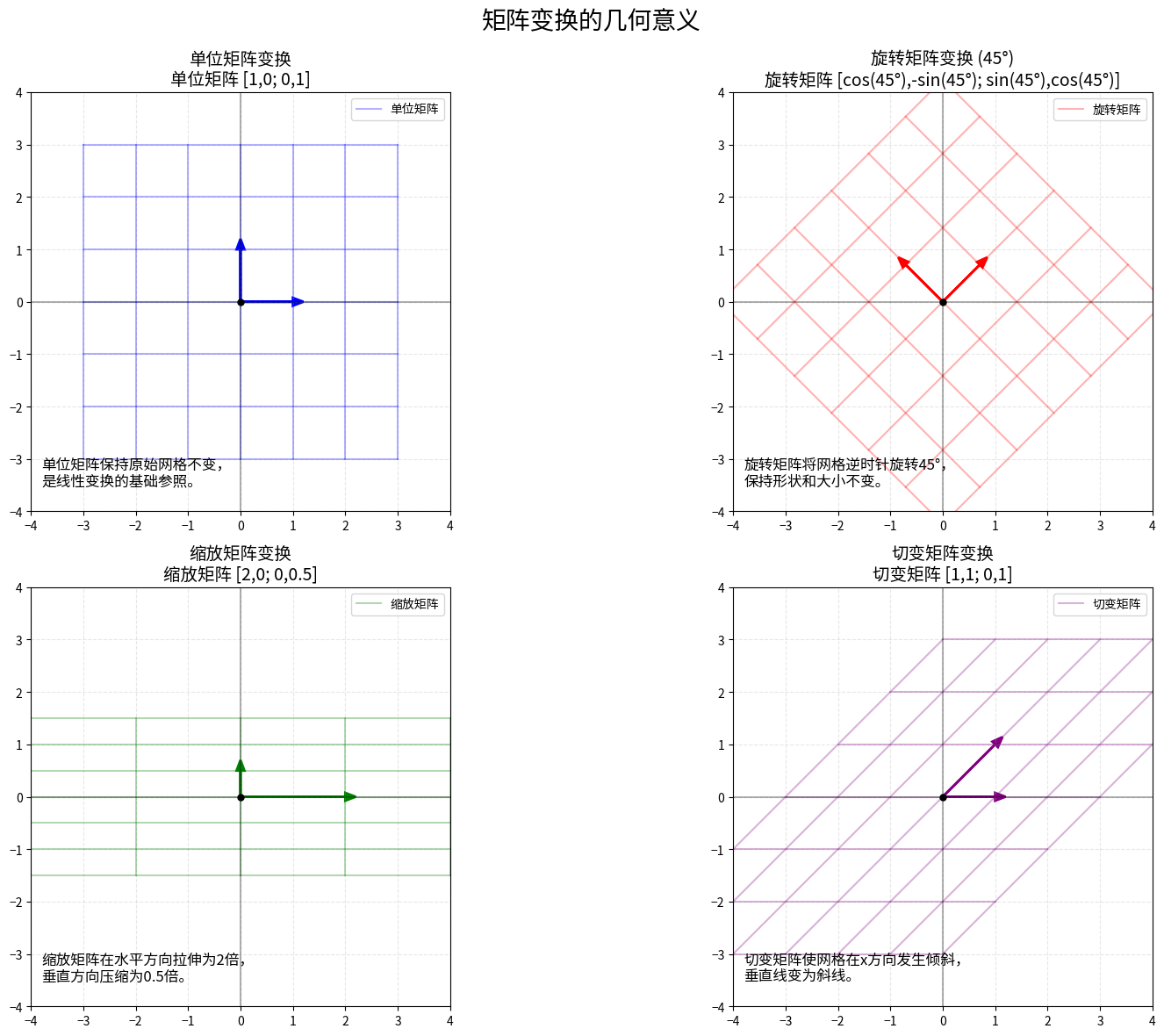
例如,2D旋转矩阵为:
R = [[cos(θ), -sin(θ)],
[sin(θ), cos(θ)]]
2D缩放矩阵为:
S = [[sx, 0],
[0, sy]]
其中sx和sy分别是x和y方向的缩放因子。
这些变换矩阵可以组合使用,例如要先旋转后缩放,只需计算S·R即可得到复合变换矩阵。在计算机图形学中,通常使用齐次坐标表示,这允许我们用矩阵乘法表示包括平移在内的所有仿射变换。
import cv2
import numpy as np
# 读取图像
image = cv2.imread('image.jpg')
# 获取图像尺寸
height, width = image.shape[:2]
# 定义旋转矩阵,旋转45度
angle = 45
rotation_matrix = cv2.getRotationMatrix2D((width/2, height/2), angle, 1)
# 应用变换
rotated_image = cv2.warpAffine(image, rotation_matrix, (width, height))
# 定义缩放矩阵,宽度缩放为原来的1.5倍,高度缩放为原来的0.8倍
scaling_matrix = np.float32([[1.5, 0, 0],
[0, 0.8, 0]])
scaled_image = cv2.warpAffine(image, scaling_matrix, (int(width*1.5), int(height*0.8)))
# 显示结果
cv2.imshow('Original', image)
cv2.imshow('Rotated', rotated_image)
cv2.imshow('Scaled', scaled_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
这些看似简单的变换背后隐藏着深刻的几何学原理。例如,旋转矩阵是正交矩阵,它保持向量的长度和向量间的角度不变。缩放矩阵是对角矩阵,它沿着坐标轴改变空间的度量。
在现代计算机视觉算法中,这些基础变换被用于各种任务,如图像配准、物体检测和三维重建。深度学习模型也经常在输入阶段使用这些变换来增强数据集,提高模型的泛化能力。
可视化的力量:用Manim动画库演示矩阵变换
理解抽象的数学概念往往依赖于强大的可视化工具。3Blue1Brown的视频系列使得线性代数概念变得直观易懂,而这些视频背后使用的是Grant Sanderson创建的Python库——Manim。
Manim允许我们创建数学动画,特别适合展示向量和矩阵变换的几何意义。例如,我们可以动态展示一个矩阵如何将一个向量或一个网格变换到新的位置。
from manim import *
class MatrixTransformation(Scene):
def construct(self):
# 创建一个网格
grid = NumberPlane()
self.add(grid)
self.wait()
# 定义变换矩阵
matrix = [[2, 1], [1, 1]]
# 应用变换
self.play(
grid.animate.apply_matrix(matrix),
run_time=3
)
self.wait()
# 显示矩阵
matrix_tex = MathTex(r"\begin{pmatrix} 2 & 1 \\ 1 & 1 \end{pmatrix}")
matrix_tex.to_corner(UL)
self.play(Write(matrix_tex))
self.wait(2)
通过动画展示,我们可以直观地看到矩阵如何改变空间中的点和线,这远比静态的公式更容易理解。例如,看到一个矩阵如何将一个圆变成椭圆,或者将一个正方形变成平行四边形,能够立即理解该矩阵的核心特性。
Manim的强大之处不仅在于动画效果,还在于它的数学表达能力。我们可以展示矩阵乘法、特征值计算、向量投影等复杂操作,让抽象的概念变得具体可见。
结语:线性代数的美与力量
当我在大学第一次接触线性代数时,它看起来只是一堆符号和规则的集合。但随着对其应用的深入了解,我开始欣赏其中的优雅和力量。线性代数是一门关于变换的学科,它告诉我们如何系统地改变空间中的点和线,而这恰恰是现代科技发展的核心需求。
从计算机图形学到量子计算,从数据压缩到机器学习,线性代数的指纹无处不在。它提供了一种语言,让我们能够表达和处理高维数据中的复杂关系。正如数学家Gilbert Strang所说:"线性代数是连接数学不同分支的纽带。"
如果你正在学习这门学科,我希望这篇文章能让你看到抽象概念背后的具体应用和几何意义。掌握线性代数不仅仅是为了通过考试,更是获得一种强大思维工具,帮助你理解和解决现实世界的问题。
回到我开头提到的那个春天午后的顿悟,正是那种对数学美的感知,让我坚持探索这个领域。线性代数的美不仅在于其内部结构的协调一致,更在于它与物理世界的奇妙契合。当你发现一个数学模型能够精确描述现实现象时,那种兴奋和满足感是无与伦比的。
让我们继续这段数学之旅,用好奇心和想象力,探索线性代数的无限可能。