当我第一次接触机器学习时,线性模型就像是一位温和的老师,用最简单的方式为我打开了数据科学的大门。那条直线看似简单,却蕴含着深刻的数学美感。今天,让我们一起踏上这段从线性回归到弹性网络的奇妙旅程。
网页版:https://iirkprbg.gensparkspace.com
视频版:https://www.youtube.com/watch?v=AIPt5UC01Gs
音频版:https://notebooklm.google.com/notebook/9206c9b2-ab11-48a7-8550-c632ebc50231/audio
最小二乘法:一切的开始
故事要从200多年前说起。那时,德国数学家高斯面对着天体观测数据的噪声问题,他提出了最小二乘法这个看似简单却极其重要的思想。想象一下,你手里有一把散落的数据点,如何找到一条最能代表它们的直线呢?
最小二乘法的核心思想是让所有数据点到直线的距离平方和最小。这个看似简单的想法,实际上蕴含着深刻的数学原理。当我们写下损失函数 J(θ) = 1/2m Σ(hθ(x) – y)² 时,我们实际上是在寻找一个使预测误差最小的参数组合。
在实际应用中,比如预测房价,我们可能会发现房屋面积和价格之间存在着近似线性的关系。通过最小二乘法,我们可以找到最佳的权重系数,让模型的预测尽可能准确。
梯度下降:寻找最优解的艺术

如果说最小二乘法告诉我们"目标是什么",那么梯度下降就是告诉我们"如何到达那里"。这个过程就像一个盲人在山坡上寻找最低点:他无法看到整个地形,只能感受脚下的坡度,然后一步步向下走。
梯度下降的数学表达式看起来很简单:θ = θ – α∇J(θ),但这个公式背后的直觉却很美妙。学习率α就像是步伐的大小,太大可能跳过最优点,太小则收敛太慢。在实际训练中,我们经常能看到损失函数随着迭代次数的增加而逐渐下降,这种收敛的过程让人着迷。
逻辑回归:从直线到曲线的转变

当我们从回归问题转向分类问题时,传统的线性回归就显得力不从心了。这时候,逻辑回归登场了。Sigmoid函数 σ(z) = 1/(1+e^(-z)) 就像一个优雅的数学变换,将任何实数值映射到0和1之间。
这个S形曲线有着迷人的性质:当输入很大时,输出接近1;当输入很小时,输出接近0;而在中间区域,它提供了平滑的过渡。这正是我们在分类问题中需要的特性。
交叉熵损失函数 J(θ) = -1/m Σ[y*log(hθ(x)) + (1-y)*log(1-hθ(x))] 的设计也很巧妙。它不仅确保了损失函数的凸性,还能很好地处理概率预测的情况。
正则化:对抗过拟合的武器
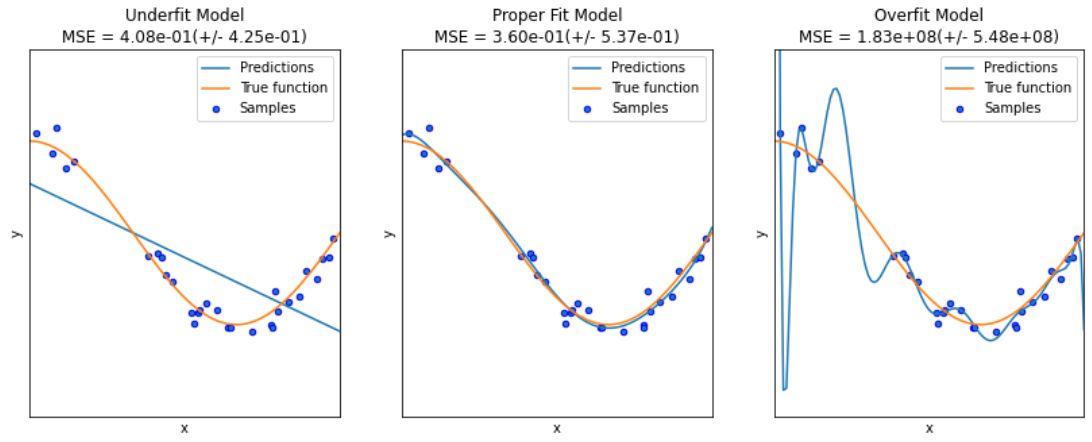
在实际应用中,我们经常会遇到一个棘手的问题:模型在训练数据上表现很好,但在新数据上却表现糟糕。这就是过拟合现象。为了解决这个问题,数学家们发明了正则化技术。
岭回归:L2正则化的智慧
岭回归在原有的损失函数基础上增加了一个L2惩罚项:J(θ) = 1/2m Σ(hθ(x) – y)² + λΣθ²。这个λΣθ²项就像一个温和的约束,它不会让任何参数完全消失,但会让所有参数都变得更小、更平滑。
这种方法特别适合处理多重共线性问题。当特征之间高度相关时,岭回归能够稳定地分配权重,避免模型过度依赖某个特征。
Lasso回归:L1正则化的特殊魅力
Lasso回归则采用了L1惩罚项:J(θ) = 1/2m Σ(hθ(x) – y)² + λΣ|θ|。这个绝对值函数有一个神奇的性质:它会让一些参数变为零,从而实现特征选择的功能。
这种"稀疏性"特性使得Lasso回归不仅能够防止过拟合,还能自动识别最重要的特征。在特征很多的情况下,这种自动特征选择的能力非常宝贵。
弹性网络:两全其美的方案
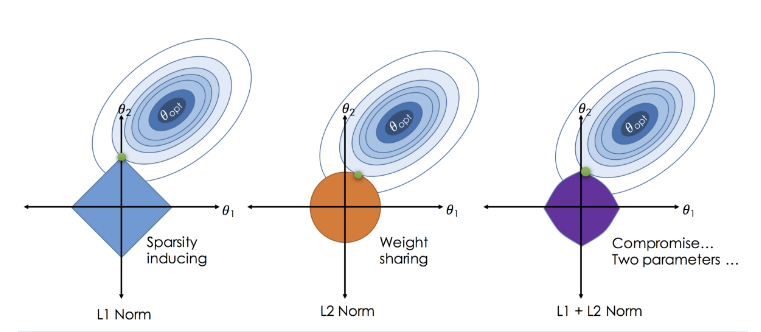
弹性网络结合了L1和L2正则化的优点:J(θ) = 1/2m Σ(hθ(x) – y)² + λ₁Σ|θ| + λ₂Σθ²。通过调节λ₁和λ₂的比例,我们可以在特征选择和稳定性之间找到平衡。
这种方法特别适合处理特征数量远大于样本数量的情况,或者当特征之间存在群组效应时。弹性网络能够选择整个相关特征组,而不是随机选择其中一个。
实践项目:理论与应用的结合
理论学习完成后,最重要的是将这些知识应用到实际项目中。
房价预测项目
在房价预测项目中,我们可以使用波士顿房价数据集或者加州房价数据集。这个项目涵盖了完整的机器学习流程:
- 数据探索:分析特征分布、相关性,识别异常值
- 特征工程:创建新特征,处理缺失值,标准化数据
- 模型比较:比较线性回归、岭回归、Lasso回归和弹性网络的性能
- 超参数调优:使用交叉验证选择最优的正则化参数
- 模型评估:使用MAE、MSE、R²等指标评估模型性能
客户流失预测项目
在客户流失预测项目中,我们使用逻辑回归来预测客户是否会流失:
- 数据预处理:处理类别变量,解决类别不平衡问题
- 特征选择:使用Lasso回归进行特征选择
- 模型训练:训练逻辑回归模型,调整决策阈值
- 性能评估:使用精确率、召回率、F1分数、AUC等指标
- 业务洞察:分析重要特征,为业务决策提供支持
可视化的力量
在学习这些模型时,可视化是理解算法本质的重要工具。我们可以通过以下几种方式来增强理解:
- 拟合过程动画:展示梯度下降如何逐步找到最优解
- 决策边界可视化:显示逻辑回归如何分离不同类别
- 正则化路径图:展示随着正则化参数变化,模型系数如何变化
- 残差分析图:诊断模型的假设是否满足
选择合适的模型
在实际应用中,选择合适的模型需要考虑多个因素:
- 数据规模:样本数量和特征数量的关系
- 特征相关性:特征之间是否存在多重共线性
- 解释性要求:是否需要模型具有良好的可解释性
- 计算资源:训练时间和预测时间的限制
一般来说,当特征数量较少且需要高解释性时,选择线性回归;当存在多重共线性时,选择岭回归;当需要特征选择时,选择Lasso回归;当需要平衡特征选择和稳定性时,选择弹性网络。
超越基础:深入理解
虽然这些模型看起来简单,但它们背后的数学原理非常深刻。理解这些模型的关键在于:
- 损失函数的设计:不同的损失函数适用于不同的问题
- 优化算法的选择:梯度下降、坐标下降、近端梯度法等
- 正则化的本质:贝叶斯观点下的先验分布
- 统计学习理论:偏差-方差权衡、VC维理论等
未来的发展方向
线性模型虽然简单,但它们是许多现代机器学习算法的基础。从线性模型出发,我们可以理解:
- 广义线性模型:扩展到不同的响应变量分布
- 核方法:通过核函数扩展到非线性情况
- 深度学习:神经网络本质上是多层线性变换的组合
- 稀疏学习:在高维数据中寻找稀疏解
结语
线性模型家族为我们提供了一个完美的学习路径:从最简单的线性回归开始,逐步引入更复杂的概念,最终掌握现代机器学习的核心思想。这个过程不仅是技术的学习,更是数学思维的训练。
当我们真正理解了这些模型的本质时,我们就能够在面对新问题时游刃有余地选择合适的方法,设计有效的解决方案。这正是机器学习的魅力所在:用数学的语言描述现实世界,用算法的力量解决实际问题。
在这个数据驱动的时代,掌握线性模型家族不仅是技术要求,更是数据科学家的基本功。从最小二乘法到弹性网络,每一个模型都是前人智慧的结晶,值得我们深入学习和理解。