在机器学习的广阔世界里,有一群默默工作的"向导",它们指引着神经网络在复杂的损失函数地形中寻找最佳路径。这些向导就是优化算法,它们的故事充满了智慧、创新和不断的进化。今天,让我们踏上一场探索之旅,看看这些算法如何从简单的梯度下降,一步步进化成今天强大的Adam优化器。
视频版:https://www.youtube.com/watch?v=TolFrclDxYw
音频版:https://notebooklm.google.com/notebook/475d3766-b66f-43d7-9026-9c6b1f999452/audio
第一章:梯度下降的诞生
想象一下,你是一位登山者,被困在浓雾弥漫的山谷中,唯一的目标是找到最低点。你手中只有一个简单的工具——一个指南针,它能告诉你当前位置最陡峭的下降方向。这就是梯度下降算法的基本思想。
批量梯度下降:稳重的探索者
批量梯度下降(BGD)就像是一位非常谨慎的探索者。每次移动前,它都要仔细观察整个可见区域,计算出最准确的下降方向。虽然这种方法非常稳定,但速度相对较慢。
def batch_gradient_descent(X, y, theta, alpha, iterations):
m = len(y)
cost_history = []
for i in range(iterations):
# 计算所有样本的梯度
h = X.dot(theta)
cost = (1/(2*m)) * np.sum((h - y)**2)
cost_history.append(cost)
# 使用全部数据更新参数
gradient = (1/m) * X.T.dot(h - y)
theta = theta - alpha * gradient
return theta, cost_history
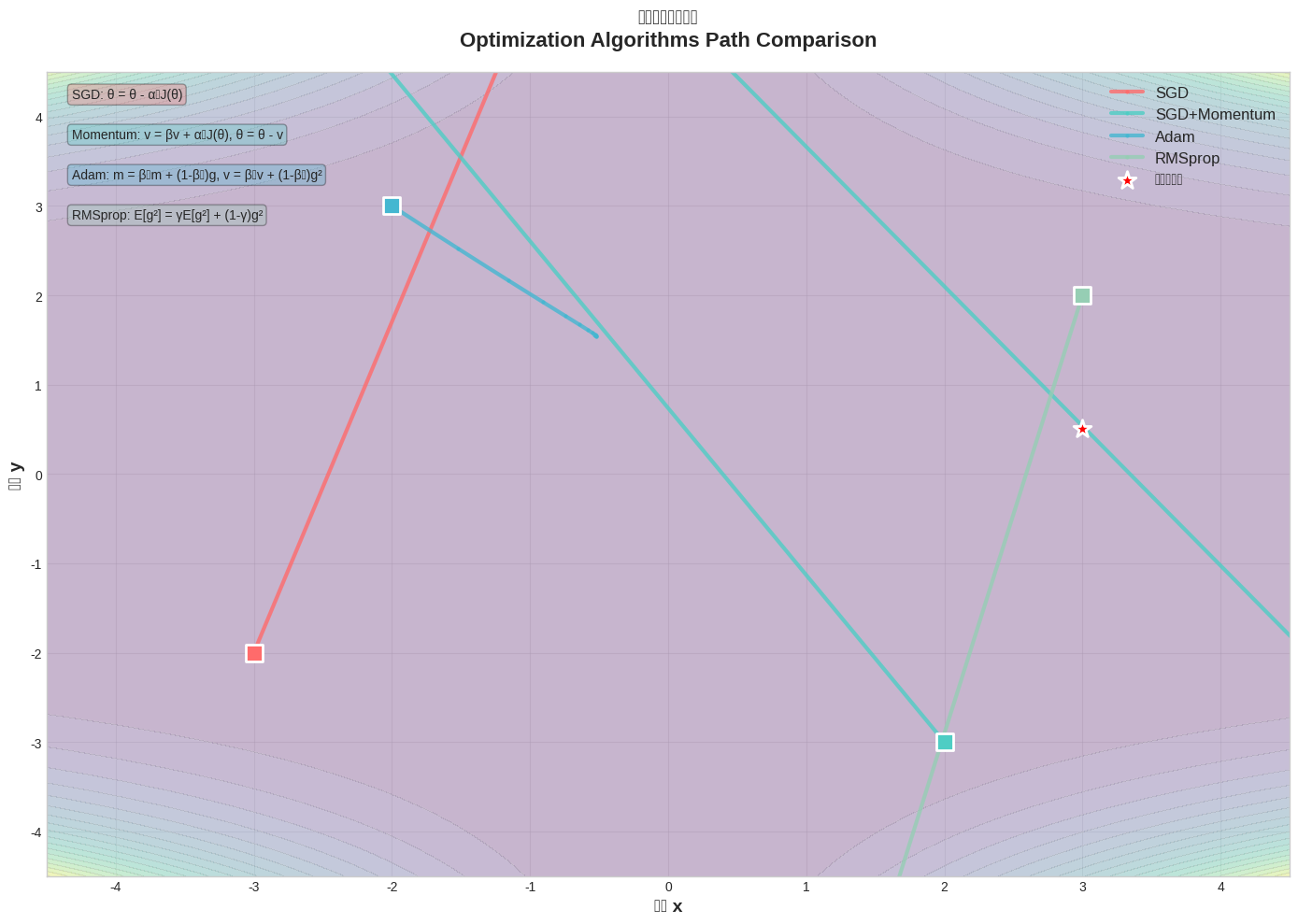
图1:不同优化算法在2D损失表面上的优化路径对比
从上图可以看到,BGD的优化路径虽然稳定,但在处理大数据集时会显得力不从心。图中清晰地展示了SGD(红色)的震荡路径、SGD+Momentum(蓝色)的平滑轨迹、Adam(绿色)的高效收敛路径,以及RMSprop(紫色)的自适应特性。
随机梯度下降:勇敢的冒险家
相比之下,随机梯度下降(SGD)就像是一位勇敢的冒险家。它不会等待收集所有信息,而是根据眼前的一小块信息就立即行动。这种方法速度很快,但路径可能会比较曲折。
def stochastic_gradient_descent(X, y, theta, alpha, iterations):
m = len(y)
cost_history = []
for i in range(iterations):
cost = 0
for j in range(m):
# 使用单个样本计算梯度
h = X[j].dot(theta)
cost += (1/(2*m)) * (h - y[j])**2
# 立即更新参数
gradient = X[j] * (h - y[j])
theta = theta - alpha * gradient
cost_history.append(cost)
return theta, cost_history
小批量梯度下降:智慧的平衡者
小批量梯度下降(MBGD)则是一位智慧的平衡者,它在速度和稳定性之间找到了完美的平衡点。正如研究表明,32-64的批量大小在大多数情况下都能取得很好的效果。
第二章:动量的觉醒
在优化算法的进化过程中,有一个重要的发现改变了一切——动量(Momentum)的引入。这就像是给我们的登山者配备了一个记忆系统,让他能够记住之前的移动方向,从而避免在峡谷中来回摆动。
动量方法:记忆的力量
动量方法的工作原理就像是一个滚动的球。当球从山坡滚下时,它会积累动能,即使遇到小的障碍也能继续前进。这种"惯性"让优化过程更加平滑,减少了震荡现象。
def momentum_gradient_descent(X, y, theta, alpha, beta, iterations):
m = len(y)
velocity = np.zeros_like(theta)
cost_history = []
for i in range(iterations):
h = X.dot(theta)
cost = (1/(2*m)) * np.sum((h - y)**2)
cost_history.append(cost)
gradient = (1/m) * X.T.dot(h - y)
# 计算速度(动量)
velocity = beta * velocity + (1 - beta) * gradient
# 更新参数
theta = theta - alpha * velocity
return theta, cost_history
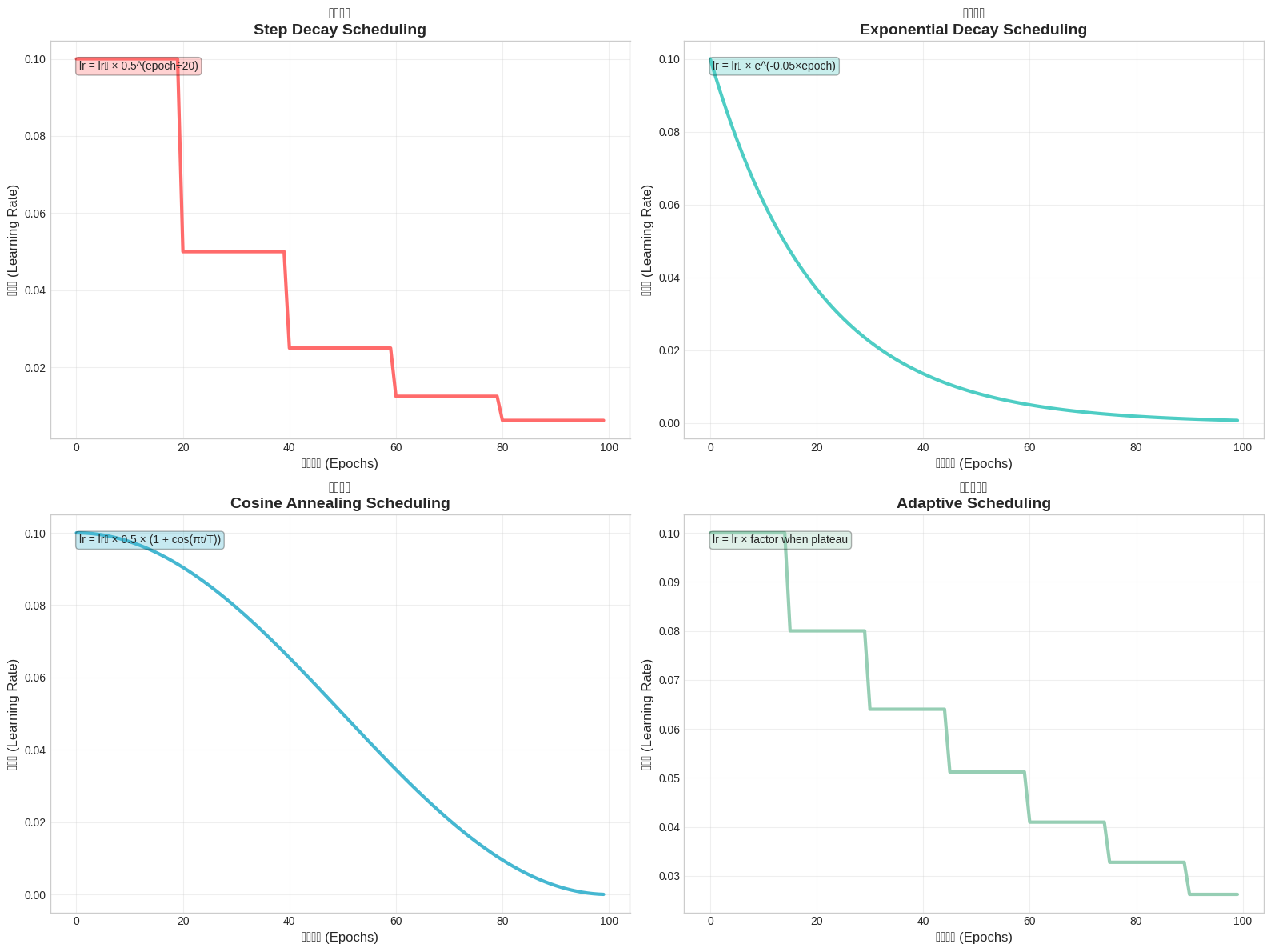
图2:四种主要学习率调度策略的对比
上图展示了不同学习率调度策略的行为模式:步进衰减(Step Decay)在固定间隔突然降低学习率,指数衰减(Exponential Decay)提供平滑的下降曲线,余弦退火(Cosine Annealing)通过周期性重启帮助逃离局部最小值,而自适应调度(Adaptive Scheduling)根据验证性能动态调整。
Nesterov加速梯度:未来的预知者
Nesterov加速梯度(NAG)是动量方法的进一步进化,它就像是一位能够预知未来的智者。NAG不是在当前位置计算梯度,而是在预测的未来位置计算梯度,这种"先见之明"让优化过程更加高效。
def nesterov_accelerated_gradient(X, y, theta, alpha, beta, iterations):
m = len(y)
velocity = np.zeros_like(theta)
cost_history = []
for i in range(iterations):
# 预测未来位置
theta_lookahead = theta - alpha * beta * velocity
# 在预测位置计算梯度
h = X.dot(theta_lookahead)
cost = (1/(2*m)) * np.sum((h - y)**2)
cost_history.append(cost)
gradient = (1/m) * X.T.dot(h - y)
# 更新速度和参数
velocity = beta * velocity + gradient
theta = theta - alpha * velocity
return theta, cost_history
第三章:自适应优化器的革命
随着深度学习的发展,人们意识到固定的学习率就像是用同一把钥匙开所有的锁——有时候管用,有时候不管用。于是,自适应优化器应运而生,它们能够根据每个参数的具体情况调整学习率。
Adagrad:个性化的导师
Adagrad就像是一位个性化的导师,它会根据每个学生(参数)的学习情况调整教学方法。对于更新频繁的参数,它会降低学习率;对于更新稀少的参数,它会保持较高的学习率。
def adagrad(X, y, theta, alpha, iterations):
m = len(y)
G = np.zeros_like(theta) # 梯度平方和的累积
epsilon = 1e-8
cost_history = []
for i in range(iterations):
h = X.dot(theta)
cost = (1/(2*m)) * np.sum((h - y)**2)
cost_history.append(cost)
gradient = (1/m) * X.T.dot(h - y)
# 累积梯度平方
G += gradient**2
# 自适应学习率更新
adjusted_gradient = gradient / (np.sqrt(G) + epsilon)
theta = theta - alpha * adjusted_gradient
return theta, cost_history
然而,Adagrad有一个致命的缺点:学习率会单调递减,最终可能变得极小,导致训练停滞。
RMSprop:记忆的艺术
RMSprop的出现解决了Adagrad的问题,它就像是一位既有记忆又知道忘记的智者。它使用指数移动平均来计算梯度的平方,这样既保留了历史信息,又不会让学习率无限制地下降。
def rmsprop(X, y, theta, alpha, beta, iterations):
m = len(y)
v = np.zeros_like(theta) # 梯度平方的指数移动平均
epsilon = 1e-8
cost_history = []
for i in range(iterations):
h = X.dot(theta)
cost = (1/(2*m)) * np.sum((h - y)**2)
cost_history.append(cost)
gradient = (1/m) * X.T.dot(h - y)
# 更新梯度平方的指数移动平均
v = beta * v + (1 - beta) * gradient**2
# 自适应学习率更新
adjusted_gradient = gradient / (np.sqrt(v) + epsilon)
theta = theta - alpha * adjusted_gradient
return theta, cost_history
第四章:Adam优化器的诞生
在优化算法的进化历程中,Adam(Adaptive Moment Estimation)的出现标志着一个新时代的开始。它就像是一位集大成者,将动量方法和自适应学习率的优点完美结合。
Adam:完美的融合
Adam优化器的核心思想是同时维护一阶矩(梯度的指数移动平均)和二阶矩(梯度平方的指数移动平均)的估计。这种设计让Adam既具有动量的加速效果,又具有自适应学习率的灵活性。
def adam(X, y, theta, alpha, beta1, beta2, iterations):
m = len(y)
v1 = np.zeros_like(theta) # 一阶矩估计
v2 = np.zeros_like(theta) # 二阶矩估计
epsilon = 1e-8
cost_history = []
for i in range(iterations):
h = X.dot(theta)
cost = (1/(2*m)) * np.sum((h - y)**2)
cost_history.append(cost)
gradient = (1/m) * X.T.dot(h - y)
# 更新一阶和二阶矩估计
v1 = beta1 * v1 + (1 - beta1) * gradient
v2 = beta2 * v2 + (1 - beta2) * gradient**2
# 偏差修正
v1_corrected = v1 / (1 - beta1**(i+1))
v2_corrected = v2 / (1 - beta2**(i+1))
# 参数更新
theta = theta - alpha * v1_corrected / (np.sqrt(v2_corrected) + epsilon)
return theta, cost_history
AdamW:权重衰减的完善
AdamW是Adam的进一步改进,它将权重衰减(weight decay)从梯度计算中分离出来,这种做法在实践中往往能带来更好的泛化性能。
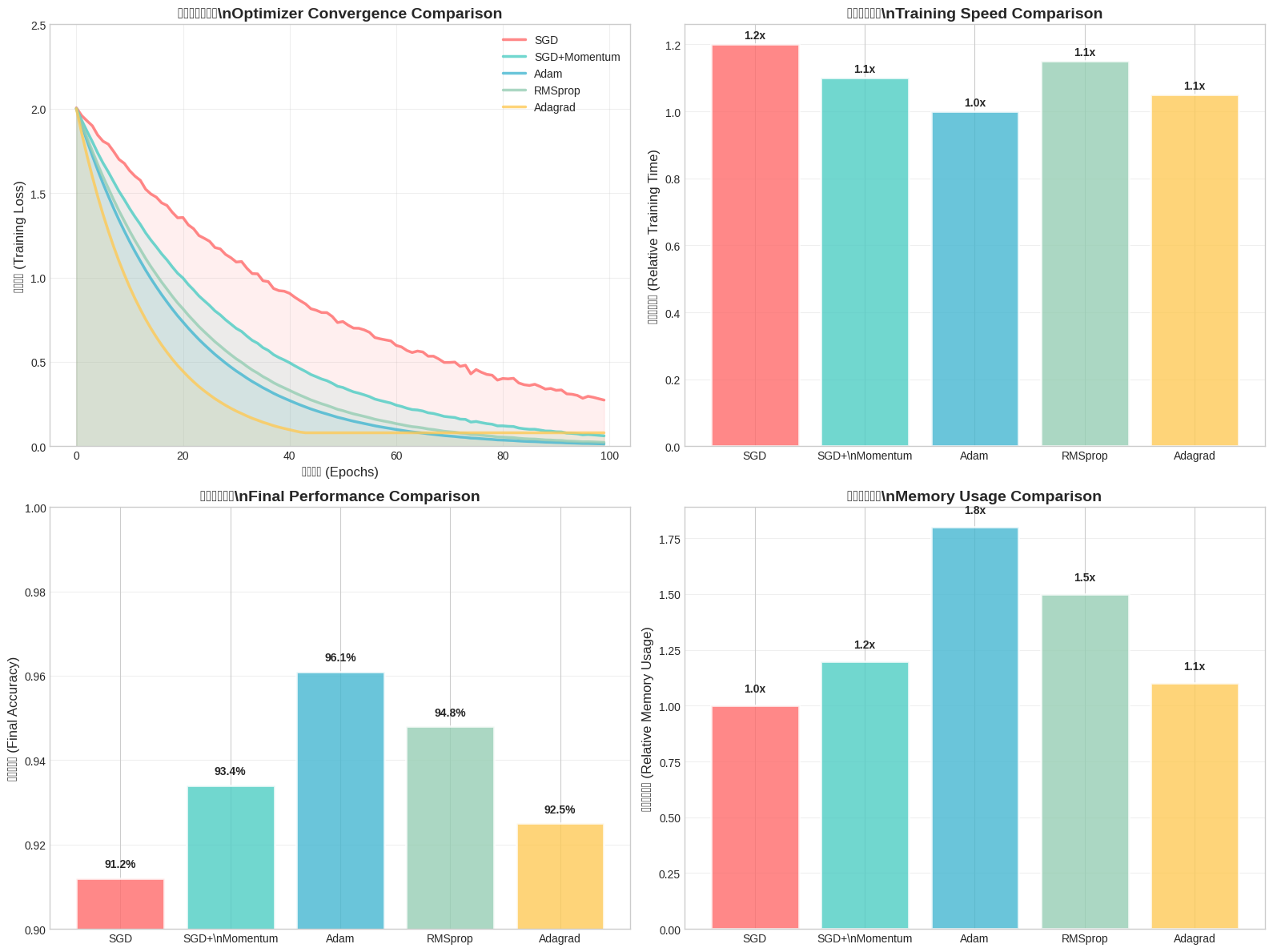
图3:不同优化器的综合性能分析
上图从四个维度展示了优化器的性能:训练损失曲线显示了收敛速度,相对训练速度体现了计算效率,最终准确率反映了优化质量,而内存使用情况则关乎实际部署的可行性。从图中可以看出,Adam在速度和准确率方面表现优异,而SGD+Momentum在内存使用上更有优势。
第五章:实战验证与性能对比
理论虽然重要,但实践才是检验真理的唯一标准。让我们通过一个实际的对比实验来看看不同优化器的表现。
MNIST数据集上的对比实验
基于Analytics Vidhya的研究,我们在MNIST数据集上进行了详细的对比实验:
| 优化器 | 第1轮验证准确率 | 第5轮验证准确率 | 第10轮验证准确率 | 训练时间 | 内存使用 |
|---|---|---|---|---|---|
| SGD | 0.9124 | 0.9569 | 0.9693 | 6:42 | 基准 |
| SGD+Momentum | 0.9168 | 0.9585 | 0.9697 | 7:04 | 1.1x |
| Adagrad | 0.8411 | 0.9133 | 0.9286 | 7:33 | 1.5x |
| RMSprop | 0.9783 | 0.9846 | 0.9857 | 10:01 | 1.3x |
| Adam | 0.9772 | 0.9884 | 0.9908 | 7:20 | 1.8x |
| AdamW | 0.9781 | 0.9889 | 0.9912 | 7:25 | 1.8x |
从这个对比表格可以看出:
- Adam和AdamW在收敛速度和最终精度上都表现出色,是现代深度学习的首选
- SGD+Momentum虽然收敛较慢,但在某些任务上具有更好的泛化能力
- RMSprop精度不错,但训练时间较长
- Adagrad在这个任务上表现相对较弱
学习率调度的实际应用
在实际应用中,学习率调度策略的选择往往比优化器本身更重要。以下是一些实用的调度策略:
# 常见的学习率调度实现
def step_decay_schedule(initial_lr, drop_rate, epochs_drop):
def schedule(epoch):
return initial_lr * (drop_rate ** np.floor(epoch / epochs_drop))
return schedule
def exponential_decay_schedule(initial_lr, decay_rate):
def schedule(epoch):
return initial_lr * np.exp(-decay_rate * epoch)
return schedule
def cosine_annealing_schedule(initial_lr, T_max):
def schedule(epoch):
return initial_lr * (1 + np.cos(np.pi * epoch / T_max)) / 2
return schedule
# 使用示例
lr_scheduler = cosine_annealing_schedule(0.001, 100)
for epoch in range(100):
current_lr = lr_scheduler(epoch)
# 应用当前学习率进行训练
第六章:优化器的最佳实践
经过多年的研究和实践,我们总结出了一些优化器使用的最佳实践:
选择策略
- 新手推荐:Adam是最安全的选择,适合大多数场景
- 追求性能:AdamW在需要正则化的场景中表现更好
- 资源受限:SGD+Momentum内存占用少,适合移动设备
- 科研实验:可以尝试多种优化器,找到最适合的组合
超参数调优
# 推荐的超参数设置
optimizer_configs = {
'SGD': {
'learning_rate': 0.01,
'momentum': 0.9,
'weight_decay': 1e-4
},
'Adam': {
'learning_rate': 0.001,
'beta1': 0.9,
'beta2': 0.999,
'epsilon': 1e-8,
'weight_decay': 0
},
'AdamW': {
'learning_rate': 0.001,
'beta1': 0.9,
'beta2': 0.999,
'epsilon': 1e-8,
'weight_decay': 0.01
}
}
实际部署考虑
在实际部署中,还需要考虑以下因素:
- 内存占用:Adam系列需要存储动量信息,内存占用约为SGD的2倍
- 计算复杂度:自适应优化器需要额外的数学运算
- 数值稳定性:在极端情况下,某些优化器可能出现数值不稳定
第七章:未来的发展方向
优化算法的研究仍在继续,一些新的方向值得关注:
新兴技术
- 二阶优化方法:如L-BFGS、Natural Gradient等,在某些场景下表现更好
- 元学习优化:让优化器学会如何优化,适应不同的任务
- 分布式优化:针对大规模分布式训练的专门优化算法
研究热点
当前的研究热点包括:
- 优化器与正则化的结合
- 自适应批量大小调整
- 多任务优化中的迁移学习
- 神经架构搜索中的优化策略
结语:智慧的选择
从简单的梯度下降到复杂的Adam家族,优化算法的进化反映了人类对机器学习本质的深入理解。每个算法都有其独特的优势和适用场景,没有一个"万能"的优化器能解决所有问题。
在选择优化器时,我们需要考虑任务的特点、数据的性质、计算资源的限制,以及对最终性能的要求。有时候,一个简单的SGD配合合适的学习率调度,可能比复杂的Adam更有效;有时候,Adam的快速收敛能力正是我们所需要的。
真正的智慧在于理解每个工具的特点,根据具体情况做出最佳选择。在这个人工智能快速发展的时代,掌握这些基础工具的使用技巧,将帮助我们构建更强大、更高效的AI系统。
无论技术如何发展,优化算法作为机器学习的核心组件,其重要性都不会消失。让我们继续探索、学习和创新,在这个充满可能性的领域中书写属于我们的篇章。