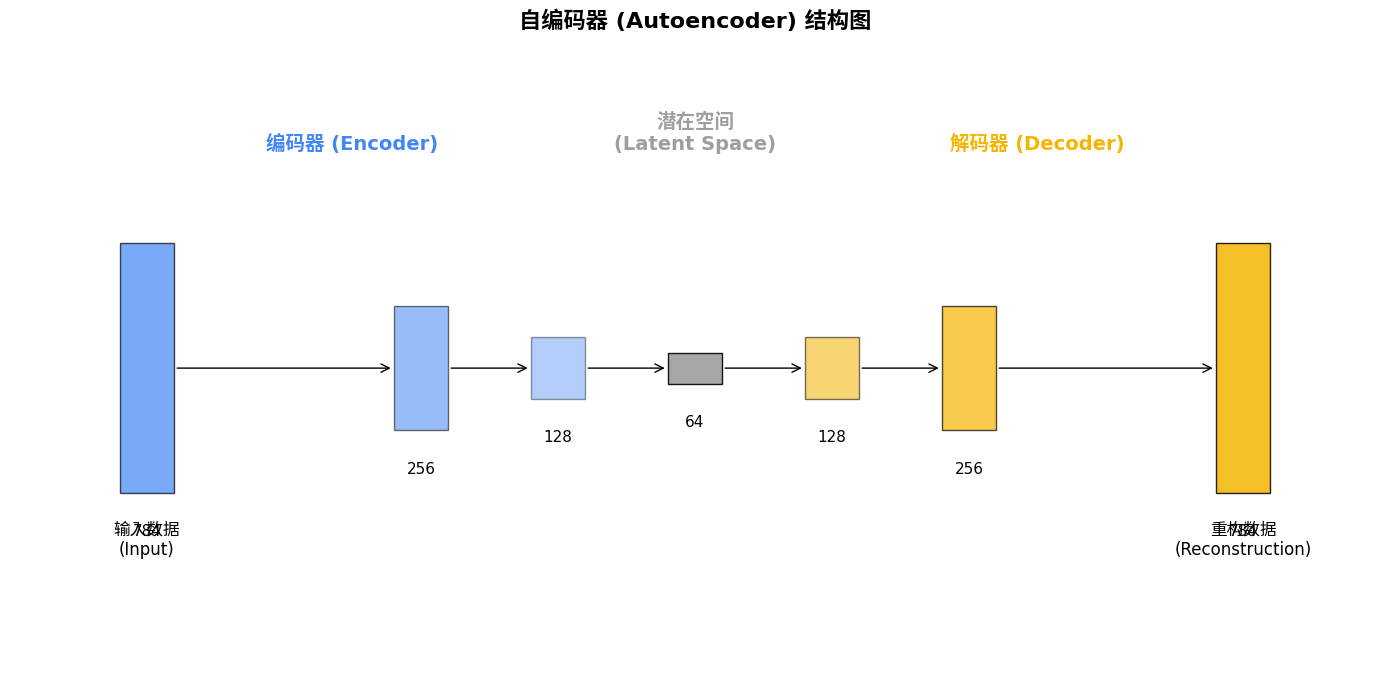
在人工智能的广阔领域中,自编码器作为一种特殊的神经网络结构,正在各个应用场景中展现出惊人的潜力。从数据降维到图像生成,从异常检测到特征提取,这个看似简单的架构却蕴含着深刻的数学原理和广泛的应用前景。今天,让我们一起揭开自编码器的神秘面纱,探索其内部机制、多样变体以及实际应用。
网页版:https://www.genspark.ai/api/page_private?id=qujljmyv
视频版:https://www.youtube.com/watch?v=Tu0hhahg0Po
音频版:https://notebooklm.google.com/notebook/d4da9b3d-d8a6-4a94-bab9-671249cac343/audio
自编码器:数据的压缩与重构艺术
自编码器本质上是一种自监督学习的神经网络,其核心思想是学习数据的有效表示。如果将数据比作一幅精美的画作,自编码器就像是先用简笔勾勒出画作的轮廓(编码过程),然后再基于这些轮廓重新绘制出完整画作(解码过程)。
基本结构与工作原理
自编码器由三个关键部分组成:
- 编码器(Encoder):将高维输入数据转换为低维表示
- 潜在空间(Latent Space):数据的压缩表示
- 解码器(Decoder):将低维表示重构回原始维度

自编码器的训练目标非常直观:最小化输入数据与重构数据之间的差异。这个差异通常通过均方误差(MSE)或二元交叉熵(BCE)等损失函数来量化。通过反向传播算法,网络参数不断调整,使重构结果越来越接近原始输入。
# 自编码器的基本损失函数
# MSE损失
reconstruction_loss = torch.mean((input_data - reconstructed_data)**2)
# 二元交叉熵损失
reconstruction_loss = F.binary_cross_entropy(reconstructed_data, input_data, reduction='mean')
潜在空间:自编码器的核心
潜在空间是自编码器的精髓所在。它是一个维度远低于原始数据的空间,却包含了重构原始数据所需的关键信息。想象一下,对于一张28×28像素的MNIST手写数字图像(784维),我们可能只需要10-20维的潜在空间就能捕获其本质特征。

潜在空间的维度选择是一个关键的超参数:
- 维度过低:重构质量下降,信息丢失严重
- 维度过高:可能失去降维的意义,甚至导致网络直接学习恒等映射
自编码器的多彩家族
随着研究的深入,自编码器家族不断壮大,涌现出多种特殊变体,各有所长。
变分自编码器(VAE):概率的艺术
变分自编码器将潜在空间视为概率分布而非确定性点,为生成能力打开了大门。

VAE不是简单地将输入编码为潜在空间中的一个点,而是编码为概率分布的参数(通常是高斯分布的均值μ和方差σ)。这种设计使得VAE具备了强大的生成能力:我们可以从潜在空间的先验分布中采样,通过解码器生成全新的数据实例。
VAE的损失函数包含两部分:
- 重构损失:衡量重构质量
- KL散度损失:使潜在空间分布接近标准正态分布
# VAE损失函数
reconstruction_loss = F.binary_cross_entropy(reconstructed_data, input_data, reduction='sum')
kl_loss = -0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
total_loss = reconstruction_loss + kl_loss

生成对抗自编码器:对抗学习的力量
结合生成对抗网络(GAN)的思想,自编码器家族又添新成员。在这种架构中,除了传统的重构损失外,还引入了判别器来区分真实样本和重构样本,促使自编码器生成更真实的输出。

GAN自编码器通常能产生比VAE更清晰、更逼真的图像,但训练过程更加复杂和不稳定。
# GAN自编码器的对抗损失
real_loss = adversarial_loss(discriminator(real_images), valid)
fake_loss = adversarial_loss(discriminator(reconstructed_images.detach()), fake)
d_loss = (real_loss + fake_loss) / 2
# 生成器损失(自编码器)
g_loss = adversarial_loss(discriminator(reconstructed_images), valid) + \
pixel_loss(reconstructed_images, real_images)
自编码器 vs PCA:老将与新秀的较量
自编码器常被与主成分分析(PCA)这一经典降维方法比较。二者各有千秋:

| 特性 | PCA | 自编码器 |
|---|---|---|
| 变换类型 | 线性 | 非线性 |
| 计算复杂度 | 低 | 高 |
| 适用数据类型 | 主要是线性可分数据 | 各种复杂数据 |
| 可解释性 | 高 | 低 |
| 扩展性 | 有限 | 极高 |
对于线性数据,PCA可能已经足够;但对于图像、音频等高度非线性数据,自编码器通常能取得更好的效果。
自编码器的实战应用
自编码器不仅仅是理论上的有趣结构,在实际应用中也展现出强大的威力。
图像压缩与重建
自编码器可以学习图像的紧凑表示,实现高效的压缩。下图展示了不同压缩率下的图像重建效果:
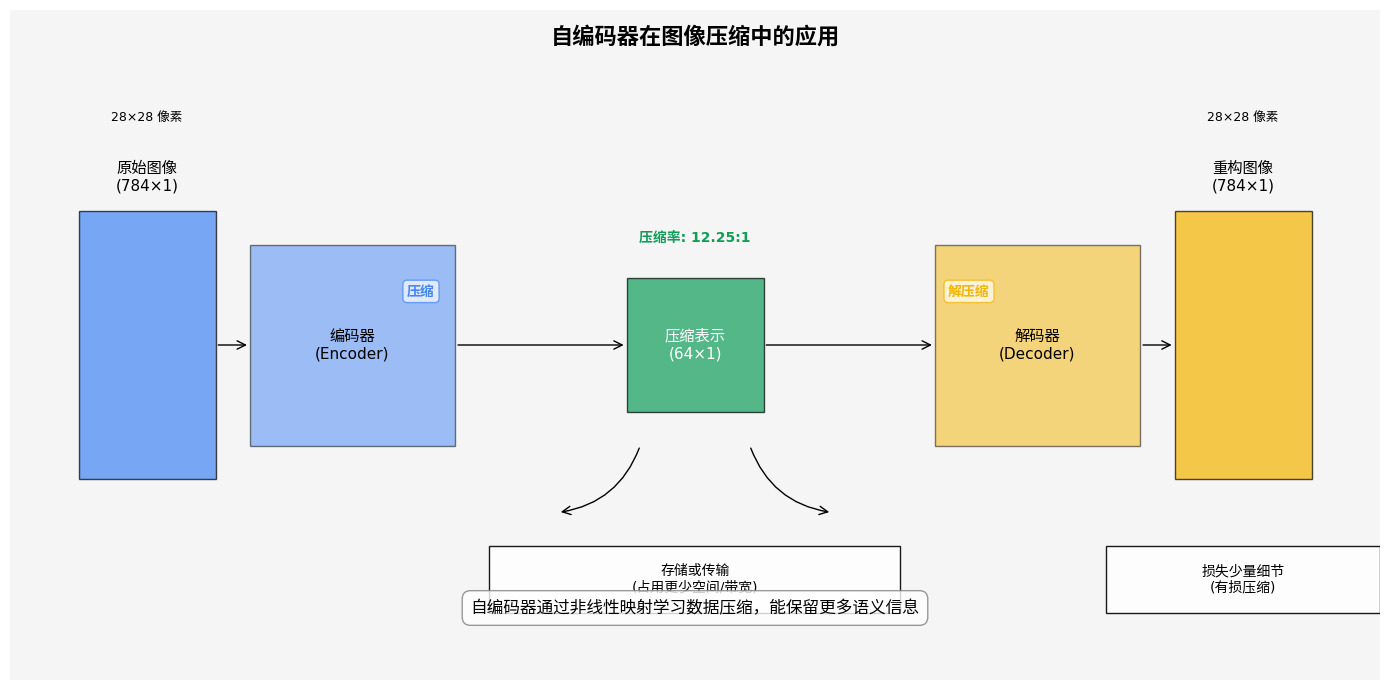
虽然在通用图像压缩方面尚无法超越JPEG等专用算法,但对于特定类型的图像(如医学影像、卫星图像),自编码器可以实现更高效的压缩。
异常检测:寻找异常的艺术
自编码器在异常检测领域大放异彩。原理很简单:用正常数据训练自编码器后,异常数据会产生较高的重构误差,因为网络没有"见过"此类模式。
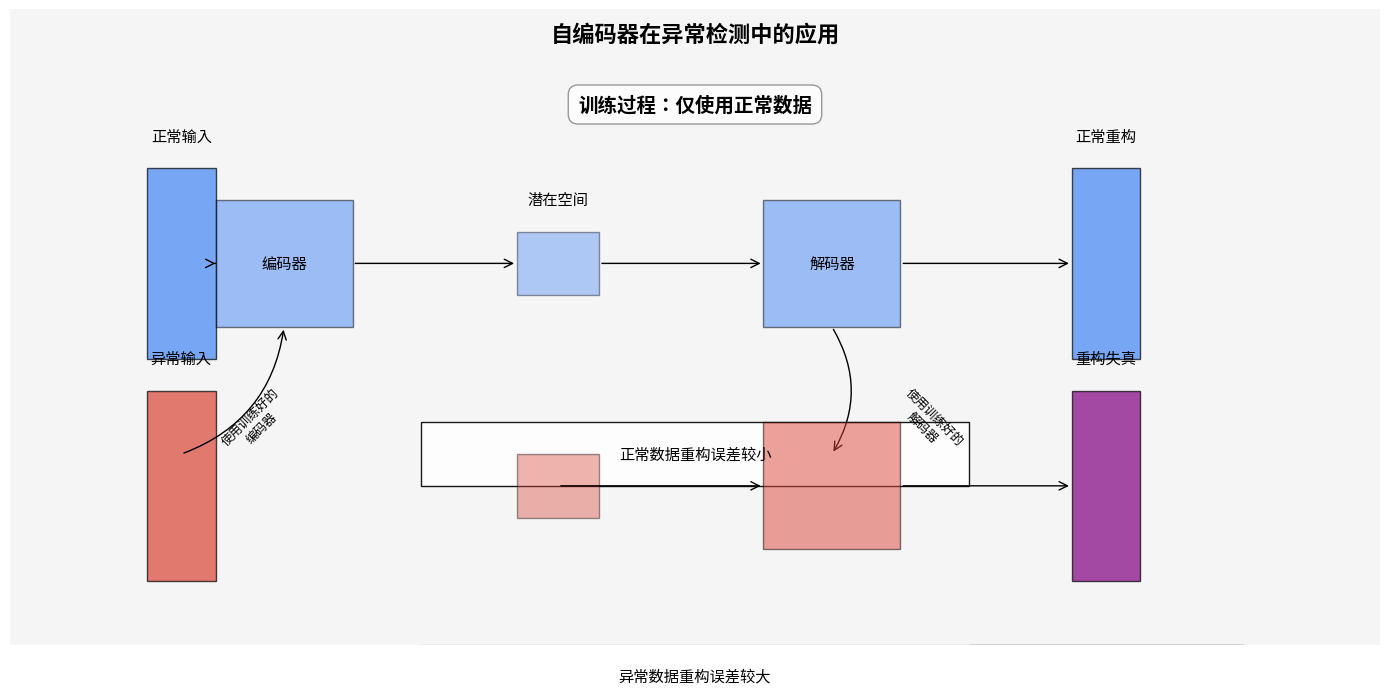
这一特性在多个领域找到应用:
- 金融欺诈检测
- 工业设备故障预测
- 网络安全入侵检测
- 医学图像中的病变识别
# 异常检测的简单实现
def detect_anomalies(autoencoder, data, threshold):
reconstructions = autoencoder(data)
mse = torch.mean((data - reconstructions)**2, dim=1)
return mse > threshold, mse
去噪与图像增强
自编码器能有效地学习从噪声数据中恢复原始信号,在图像去噪、修复等任务中表现出色。

去噪自编码器的训练略有不同:输入是加噪声的数据,而目标是原始无噪声数据。这使得网络学会过滤噪声,保留关键信息。
PyTorch实现:从理论到代码
让我们动手实现一个基于PyTorch的简单自编码器,用于MNIST手写数字数据集:
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
import matplotlib.pyplot as plt
# 定义自编码器模型
class Autoencoder(nn.Module):
def __init__(self):
super(Autoencoder, self).__init__()
# 编码器
self.encoder = nn.Sequential(
nn.Linear(28*28, 256),
nn.ReLU(True),
nn.Linear(256, 128),
nn.ReLU(True),
nn.Linear(128, 64),
nn.ReLU(True)
)
# 解码器
self.decoder = nn.Sequential(
nn.Linear(64, 128),
nn.ReLU(True),
nn.Linear(128, 256),
nn.ReLU(True),
nn.Linear(256, 28*28),
nn.Sigmoid() # 像素值归一化到[0,1]
)
def forward(self, x):
x = self.encoder(x)
x = self.decoder(x)
return x
# 数据加载
transform = transforms.Compose([
transforms.ToTensor()
])
train_dataset = datasets.MNIST('./data', train=True, download=True, transform=transform)
test_dataset = datasets.MNIST('./data', train=False, transform=transform)
train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=128, shuffle=False)
# 初始化模型
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = Autoencoder().to(device)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
# 训练模型
def train(epoch):
model.train()
train_loss = 0
for data, _ in train_loader:
data = data.view(data.size(0), -1).to(device)
optimizer.zero_grad()
output = model(data)
loss = criterion(output, data)
loss.backward()
optimizer.step()
train_loss += loss.item() * data.size(0)
return train_loss / len(train_loader.dataset)
# 测试模型
def test():
model.eval()
test_loss = 0
with torch.no_grad():
for data, _ in test_loader:
data = data.view(data.size(0), -1).to(device)
output = model(data)
loss = criterion(output, data)
test_loss += loss.item() * data.size(0)
return test_loss / len(test_loader.dataset)
# 训练过程
num_epochs = 10
train_losses = []
test_losses = []
for epoch in range(1, num_epochs + 1):
train_loss = train(epoch)
test_loss = test()
train_losses.append(train_loss)
test_losses.append(test_loss)
print(f'Epoch: {epoch}, Train Loss: {train_loss:.6f}, Test Loss: {test_loss:.6f}')
# 可视化损失曲线
plt.figure(figsize=(10, 5))
plt.plot(train_losses, label='Train Loss')
plt.plot(test_losses, label='Test Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.grid(True)
plt.show()
# 可视化重建结果
def visualize_reconstruction():
model.eval()
with torch.no_grad():
data, _ = next(iter(test_loader))
data = data[:10] # 选择10个样本
data_flat = data.view(data.size(0), -1).to(device)
output = model(data_flat)
output = output.view(data.size())
# 绘制原始图像和重构图像
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# 原始图像
ax = plt.subplot(2, n, i+1)
plt.imshow(data[i].squeeze().cpu().numpy(), cmap='gray')
plt.title('Original')
plt.axis('off')
# 重构图像
ax = plt.subplot(2, n, i+n+1)
plt.imshow(output[i].squeeze().cpu().numpy(), cmap='gray')
plt.title('Reconstructed')
plt.axis('off')
plt.tight_layout()
plt.show()
visualize_reconstruction()
执行上述代码后,我们将看到模型的训练损失曲线以及原始图像与重构图像的对比:
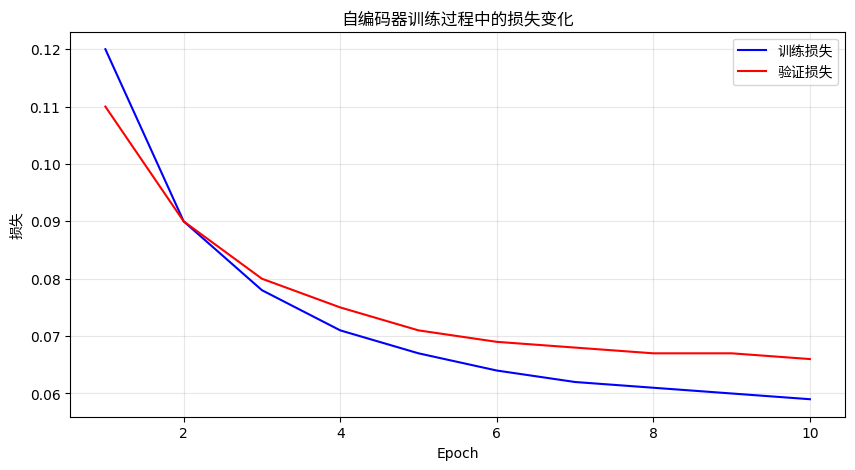

TensorFlow实现变分自编码器(VAE)
下面是使用TensorFlow/Keras实现变分自编码器的代码示例:
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import numpy as np
import matplotlib.pyplot as plt
# 参数设置
latent_dim = 2 # 潜在空间维度
input_shape = (28, 28, 1) # 输入图像形状
# 编码器网络
encoder_inputs = keras.Input(shape=input_shape)
x = layers.Conv2D(32, 3, activation="relu", strides=2, padding="same")(encoder_inputs)
x = layers.Conv2D(64, 3, activation="relu", strides=2, padding="same")(x)
x = layers.Flatten()(x)
x = layers.Dense(16, activation="relu")(x)
# 潜在空间分布参数
z_mean = layers.Dense(latent_dim, name="z_mean")(x)
z_log_var = layers.Dense(latent_dim, name="z_log_var")(x)
# 采样函数
def sampling(args):
z_mean, z_log_var = args
batch = tf.shape(z_mean)[0]
dim = tf.shape(z_mean)[1]
epsilon = tf.keras.backend.random_normal(shape=(batch, dim))
return z_mean + tf.exp(0.5 * z_log_var) * epsilon
z = layers.Lambda(sampling, output_shape=(latent_dim,), name="z")([z_mean, z_log_var])
# 编码器模型
encoder = keras.Model(encoder_inputs, [z_mean, z_log_var, z], name="encoder")
# 解码器网络
latent_inputs = keras.Input(shape=(latent_dim,))
x = layers.Dense(7 * 7 * 64, activation="relu")(latent_inputs)
x = layers.Reshape((7, 7, 64))(x)
x = layers.Conv2DTranspose(64, 3, activation="relu", strides=2, padding="same")(x)
x = layers.Conv2DTranspose(32, 3, activation="relu", strides=2, padding="same")(x)
decoder_outputs = layers.Conv2D(1, 3, activation="sigmoid", padding="same")(x)
# 解码器模型
decoder = keras.Model(latent_inputs, decoder_outputs, name="decoder")
# VAE模型
outputs = decoder(encoder(encoder_inputs)[2])
vae = keras.Model(encoder_inputs, outputs, name="vae")
# 添加KL散度损失
reconstruction_loss = tf.reduce_mean(
keras.losses.binary_crossentropy(
tf.keras.backend.flatten(encoder_inputs),
tf.keras.backend.flatten(outputs)
)
)
reconstruction_loss *= 28 * 28
kl_loss = 1 + z_log_var - tf.square(z_mean) - tf.exp(z_log_var)
kl_loss = tf.reduce_mean(kl_loss)
kl_loss *= -0.5
vae_loss = reconstruction_loss + kl_loss
vae.add_loss(vae_loss)
vae.compile(optimizer="adam")
# 加载数据
(x_train, _), (x_test, _) = keras.datasets.mnist.load_data()
x_train = x_train.astype("float32") / 255
x_test = x_test.astype("float32") / 255
x_train = np.reshape(x_train, (-1, 28, 28, 1))
x_test = np.reshape(x_test, (-1, 28, 28, 1))
# 训练VAE
history = vae.fit(x_train, x_train, epochs=10, batch_size=128, validation_data=(x_test, x_test))
# 可视化潜在空间
def plot_latent_space(encoder, decoder):
# 显示潜在空间的网格采样生成结果
n = 15 # 网格维度
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
# 在[-4, 4]范围内线性采样n个点
grid_x = np.linspace(-4, 4, n)
grid_y = np.linspace(-4, 4, n)[::-1]
for i, yi in enumerate(grid_y):
for j, xi in enumerate(grid_x):
z_sample = np.array([[xi, yi]])
x_decoded = decoder.predict(z_sample)
digit = x_decoded[0].reshape(digit_size, digit_size)
figure[i * digit_size : (i + 1) * digit_size,
j * digit_size : (j + 1) * digit_size] = digit
plt.figure(figsize=(10, 10))
plt.imshow(figure, cmap="Greys_r")
plt.axis("off")
plt.title("VAE生成的数字网格")
plt.show()
# 调用可视化函数
plot_latent_space(encoder, decoder)
执行上述代码后,我们可以看到VAE在二维潜在空间中生成的数字网格,展示了潜在空间的连续性:

自编码器、VAE与GAN的对比
下面是三种不同生成模型的比较:

每种模型都有其独特的优势和局限性:
- 普通自编码器:结构简单,重构质量高,但不具备生成能力
- 变分自编码器(VAE):具备生成能力,潜在空间连续且平滑,但生成图像常模糊
- 生成对抗网络(GAN):生成质量最高,图像锐利真实,但训练困难,易模式崩溃
自编码器的优势与局限
优势
- 非线性映射能力:相比PCA等线性方法,能捕捉更复杂的数据模式
- 多功能性:单一架构适用于多种任务(降维、去噪、生成等)
- 无监督学习:无需标记数据,可充分利用大量未标注数据
- 灵活的架构设计:可根据不同任务定制网络结构
局限
- 训练复杂度:需要更多计算资源和专业知识
- 超参数敏感:性能对潜在空间维度等超参数敏感
- 黑盒特性:潜在空间特征难以直接解释
- 图像质量问题:基本自编码器和VAE的重构/生成图像常有模糊现象
未来展望:自编码器的发展方向
自编码器技术仍在快速发展,多个方向值得期待:
- 与Transformer架构融合:增强处理序列数据的能力
- 多模态学习:在统一潜在空间中表示不同类型的数据(图像、文本、音频)
- 自监督学习的新范式:通过设计更巧妙的预训练任务提高特征学习能力
- 可解释性研究:探索潜在空间的语义含义,增强透明度
自编码器以其简洁而优雅的设计,在机器学习领域占据了重要地位。从最基础的降维工具到复杂的生成模型,自编码器展现了神经网络强大的表示学习能力。尽管存在一些局限性,但随着研究的深入和技术的演进,自编码器必将在更广阔的应用场景中发挥关键作用。
无论你是数据科学的入门者还是经验丰富的研究者,了解并掌握自编码器技术都将为你的工具箱增添一件强大武器。正如它的名字所暗示的那样——自编码器是一种能够自我学习数据表示的智能体,它不仅能压缩信息,更能捕捉数据的本质。
下次当你面对复杂的高维数据时,不妨考虑使用自编码器,或许它能为你打开新的思路和视角。